3.7 Square, Rectangle and Rhombus
These are special cases of parallelogram. Hence they have all the properties of a parallelogram and some additional properties.
Rectangle
A parallelogram in which each angle is 900 is called a rectangle. Hence a rectangle has all the properties of a parallelogram.
1) The opposite sides are parallel and congruent.
2) Diagonals bisect each other.
Apart from these the rectangle has one salient property.
Theorem: The diagonals of a rectangle are congruent. Figure 3.20 shows a rectangle.
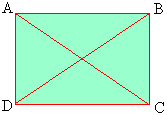
Figure 3.20
To prove that seg.AC @ seg.BD consider D ACD and D BDC . Both are right triangles.
seg.AD @ seg.BC by definition
seg.DC @ seg.CD same side
Ð ADC @ Ð BCD - both are right angles.
\D ACD @ D BDC ( SAS )
Therefore, AC @ BD corresponding sides of congruent triangles are congruent. Therefore, the diagonals of a rectangle are congruent The converse of this theorem is used as a test for rectangle.
Theorem: A parallelogram is a rectangle, if its diagonals are congruent. Figure 3.21 shows a parallelogram LMNO whose diagonals are congruent.
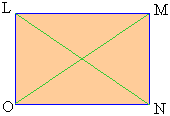
Figure 3.21
|