|
To prove that LMNO is a rectangle, consider D LNO and D MON.
seg.LN @ seg.MO given seg.LO @ seg.MN opposite sides of a parallelogram and seg.ON @ seg.NO same side
\ D LNO @ D MON ( SSS )
Ð LON @ Ð MNO ( corresponding angles of congruent triangles ). Since they are interior angles of parallel lines they are supplementary.
\ Ð LON and Ð MNO are both right angles.
\ Ð MNO is a rectangle.
Rhombus
A rhombus is defined as a quadrilateral with all sides congruent. Figure 3.20 shows a rhombus. ABCD where seg.AB @ seg.BC @ seg.CD @ seg.DA. A rhombus has all properties of a parallelogram and some more.
Additional properties of a rhombus
Theorem : The diagonals of a rhombus are perpendicular to each other. Figure 3.20 shows a rhombus ABCD.
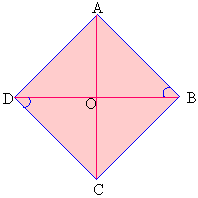
Figure 3.22
To prove that seg.AC is perpendicular to seg.BD, consider D BOA and D BOC.
seg.BA @ seg.BC definition of rhombus .......................... (1)
Ð ABD @ Ð CDB alternate angles. Ð DBC @ Ð CDB as seg.CD and seg.CB are congruent. Therefore D CBD is isosceles .
\ Ð ABD @ Ð DBC which is the same as Ð ABO @ Ð CBO ................. (2)
seg.BO @ seg.BO same side .......................... (3)
|
Index
3.
1 Definition
3.
2 Terminology
3.
3 Sum Of Interior Angles Of A Polygon
3.
4 Sum Of Exterior Angles Of A Polygon
3.
5 Trapezoids
3.
6 Parallelogram
3.
7 Square, Rectangle And Rhombus
Chapter
4
|