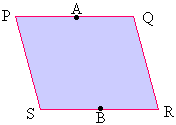
PQRS is a parallelogram where A is the midpoint of PQ and B is the midpoint of SR. Prove that PABS is a parallelogram.
Solution:
Since A and B are both equidistant from seg.PS, seg.QR and seg.AB is parallel to seg.PS. Since seg.PQ çç seg.SR, seg.PA çç seg.SB. Therefore PABS is a parallelogram as both pairs of opposite sides are parallel.
Example 3
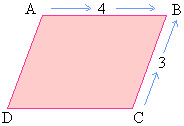
ABCD is a parallelogram
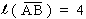
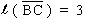
Find length 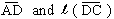
Solution:
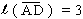 ,
, 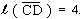
Example 4
In a parallelogram ABCD, m Ð A = x0, m Ð B = ( 3x0 + 200 ), Find x, m Ð C and
m Ð D.
Solution:
m Ð A + m Ð B = 1800
x0 + 3x0 + 200 = 1800
4x0 = 1600, x = 400
m Ð A = 400, m Ð B = 1400
Hence m Ð C = 400 and m Ð D = 1400
Example 5
Which of the following statements are true ?
a) Every rectangle is a parallelogram
b) Every rhombus is a rectangle
c) Every square is a rhombus
d) Every rectangle which is a rhombus is a square.
e) Every square is a parallelogram
f) The diagonals of a parallelogram are congruent.
Solution:
a) True
b) False
c) True
d) True
e) True
f) False
**********