|
9.4 Distances and Distance Formula
With the help of x and y axis we saw how the position of a point in the co-ordinate plane was determined. We shall now extend this theory to calculate the distances between any two points in the co-ordinate plane.
Let A (x, y) and B (x2, y2) be two points in the co-orrdinate plane as shown below :
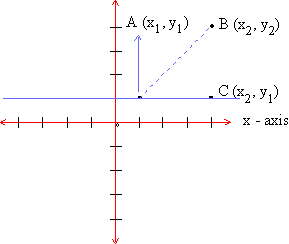
Figure 9.4
In order to find the distance between points A and B we go through following steps and use the distance formula.
Step 1 Draw a line parallel to x-axis through the point A and
draw a line parallel to y-axis through point B such that
they intersect at point C.
Step 2 We now have a right triangle with seg AB as the
hypotenuse. Therefore, by Pythagorean theorem,
(AB)2 = (AC)2 + (BC)2
\
AB = 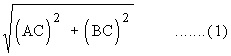
Step 3 The co-ordinates of point C can be determined
as (x2, y1).
Step 4 The distance between A and C is,
AC = (x2, x1)
\
(AC)2 = (x2, x1)2 and
The distance between B & C is
BC = (y2, y1)
\
(BC)2 = (y2, y1)2
Step 5 Substituting the values of (AC)2 and
(BC)2 in
eg (1) we get
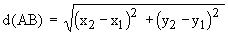
This is the distance formula.
[next
page]
|