|
9.7 Equation of a line
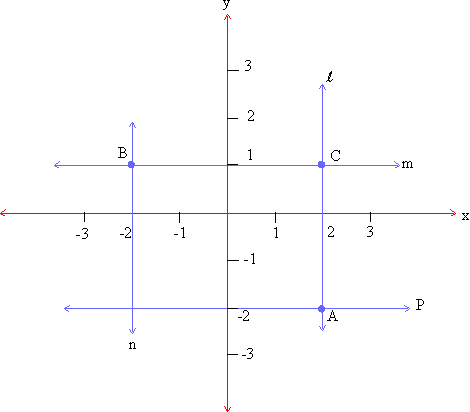
Observe the following co-ordinate plane for the values of the marked points.
Click here to enlarge
The observations are :
a) The co-ordinates of points B & C are B (-2, 1) & C (2, 1)
b) The co-ordinates of point A & C are A (2, -2) & C (2, 1 ).
Note that the x- co-ordinate value on the line l is the same for all the points on that line. This means that it satisfies the equation x = 2 for all its points.
Similarly the equation y = 1 holds true for all the points on the line m in both the cases above. We have considered lines that were parallel to the x-axis and the y-axis and hence their equations appear in one variable. If a slanted line intersecting both x and y-axis is considered then the equation would involve two variables and the equation can be written in the form of Ax + By = C, where A, B & C are real numbers.
In general, an equation of the type Ax + By = C can be graphed on a co-ordinate plane by substituting different values for x and y. If the graph is a straight line then the equation is said to be linear.
If any other point lies on this line, then its co-ordinate will make the equation a true statement. This form of an equation is called the standard form for the equation of the line.
X- Intercept and Y- Intercept : The x-intercept of a graph is the point where the graph intersects the x axis. The y co-ordinate of this point is always zero.
**********
[next page]
|