The most fundamental geometric form is a point. It is represented as a dot with a capital alphabet which is its name (Figure 1.1) A line is a set of points and it extends in opposite directions up to infinity. It is represented by two points on the line and a double headed arrow or a single alphabet in the lower case (Figure 1.1) A plane is a two dimensional (flat) surface that extends in all directions up to infinity.

A plane has obviously no size and definitely no shape. However it is represented as a quadrangle and a single capital letter (Figure 1.1)

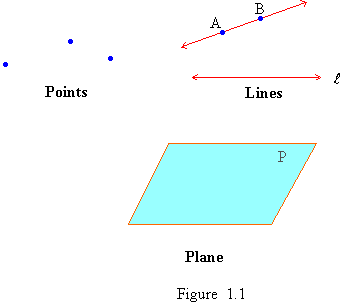
Figure 1.1 shows points A, D & Q, line AB, line l and plane P.

Some axioms regarding points, lines and planes are given below.

1. An infinite number of lines can be drawn through any given point.

2. One and only one line can be drawn through two distinct points.

3. When two lines intersect they do so at only one point.

Collinear And Coplanar

Three or more points are said to be collinear if a single line contains all of them. Otherwise they are said to be non collinear. (Figure 1.2)

Index

Introduction

1.1 Points, Lines and Planes
1.2 Line Segment
1.3 Rays and Angles
1.4 Some Special Angles
1.5 Angles made by a Transversal
1.6 Transversal Across Two Parallel Lines
1.7 Conditions for Parallelism

Chapter 2