4.3 Properties Of Arithmetic Mean
The sum of the deviations, of all the values of x, from their arithmetic mean, is zero.
Justification : 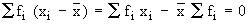
Since 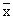 is a constant, is a constant, 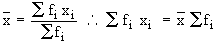
- The product of the arithmetic mean and the number of items gives the total
of all items.
Justification : 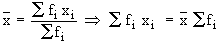
or 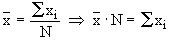
- If
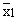 and and 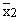 are
the arithmetic mean of two samples of sizes n1 and
n2 respectively then, the arithmetic mean are
the arithmetic mean of two samples of sizes n1 and
n2 respectively then, the arithmetic mean 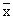 of
the distribution combining the two can be calculated as of
the distribution combining the two can be calculated as
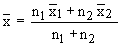
This formula can be extended for still more groups or samples.
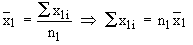
Justification : 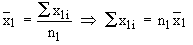 = total of the observations of the first sample = total of the observations of the first sample
Similarly 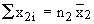 = total of the observations of the first sample = total of the observations of the first sample
The combined mean of the two samples
= 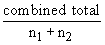
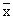 = = 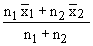
Example The average marks of three batches of students
having 70, 50 and 30 students respectively are 50, 55 and 45. Find
the average marks of all the 150 students, taken together.
Solution :
Let x be the average marks of all 150 students taken together.
Batch - I Batch - II Batch
- III
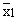 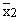 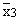
A. marks : = 50 = 55 = 45
No. of students n1 = 70 n2 = 50 n3 = 30
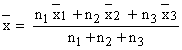 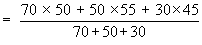
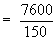
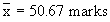
|
Index
4.1 Introduction
4.2 Arithmetic Mean
4.3 Properties of Arithmetic Mean
4.4 Median
4.5 Mode
4.6 Empirical relation between mean, median & mode
Chapter 5
|