4.4 Median
It is the value of the size of the central item of the arranged data (data arranged in the ascending or the descending order). Thus, it is the value of the middle item and divides the series in to equal parts.
In Connorís words - "The median is that value of the variable
which divides the group into two equal parts, one part comprising
all values greater and the other all values lesser than the median."
For example, the daily wages of 7 workers are 5, 7, 9, 11, 12, 14
and 15 dollars. This series contains 7 terms. The fourth term i.e.
$11 is the median.
Median In Individual Series (ungrouped Data)
Set the individual series either in the ascending (increasing) or in the descending (decreasing) order, of the size of its items or observations.
If the total number of observations be 'n' then
If 'n' is odd,
The median = size of 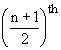 observation observation
-
If 'n' is even, the median
= 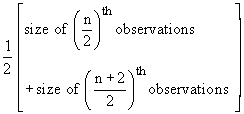
Example The following figures represent
the number of books issued at the counter of a Statistics library
on 11 different days. 96, 180, 98, 75, 270, 80, 102, 100, 94, 75
and 200. Calculate the median.
Solution:
Arrange the data in the ascending order as 75, 75, 80, 94, 96, 98, 100, 102,180, 200, 270.
Now the total number of items 'n'= 11 (odd)
Therefore, the median = size of 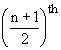 item item
= size of 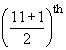 item
item
= size of 5th
item
= 98 books per day
Example The population (in thousands) of
36 metropolitan cities are as follows :
2468, 591, 437, 20, 213, 143, 1490, 407, 284, 176, 263, 19, 181, 777, 387, 302, 213, 204, 153, 733, 391, 176 178, 122, 532, 360, 65, 260, 193, 92, 672, 258, 239, 160, 147, 151. Calculate the median.
Solution:
Arranging the terms in the ascending order as :
20, 65, 92, 131, 142, 143, 147, 151, 153, 160, 169, 176, 178, 181, 193, 204, (213, 39), 258, 263, 260, 384, 302, 360, 387, 391, 407, 437, 522, 591, 672, 733, 777, 1490, 2488.
Since total number of items n = 36 (Even).
the median = 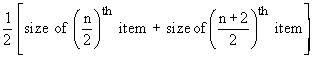

|
Index
4.1 Introduction
4.2 Arithmetic Mean
4.3 Properties of Arithmetic Mean
4.4 Median
4.5 Mode
4.6 Empirical relation between mean, median & mode
Chapter 5
|