CHAPTER 5 : MEASURES OF DISPERSION
5.1 Introduction
The measures of central tendencies (i.e. means) indicate the general magnitude of the data and locate only the center of a distribution of measures. They do not establish the degree of variability or the spread out or scatter of the individual items and their deviation from (or the difference with) the means.
i) According to Nciswanger, "Two distributions of statistical data may be symmetrical and have common means, medians and modes and identical frequencies in the modal class. Yet with these points in common they may differ widely in the scatter or in their values about the measures of central tendencies."
ii) Simpson and Kafka said, "An average alone does not tell the full story. It is hardly fully representative of a mass, unless we know the manner in which the individual item. Scatter around it .... a further description of a series is necessary, if we are to gauge how representative the average is."
From this discussion we now focus our attention on the scatter or variability which is known as dispersion. Let us take the following three sets.
|
Students |
Group X |
Group Y |
Group Z |
|
1 |
50 |
45 |
30 |
|
2 |
50 |
50 |
45 |
|
3 |
50 |
55 |
75 |
|
\ mean 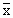 Þ
Þ
|
50 |
50 |
50 |
Thus, the three groups have same mean i.e. 50. In fact the
median of group X and Y are also equal. Now if one would say that
the students from the three groups are of equal capabilities, it
is totally a wrong conclusion then. Close examination reveals that
in group X students have equal marks as the mean, students from
group Y are very close to the mean but in the third group Z, the
marks are widely scattered. It is thus clear that the measures of
the central tendency is alone not sufficient to describe the data.
Definition of dispersion : The arithmetic mean of the deviations of the values of the individual items from the measure of a particular central tendency used. Thus the ’dispersion’ is also known as the "average of the second degree." Prof. Griffin and Dr. Bowley said the same about the dispersion.
In measuring dispersion, it is imperative to know the amount of variation (absolute measure) and the degree of variation (relative measure). In the former case we consider the range, mean deviation, standard deviation etc. In the latter case we consider the coefficient of range, the coefficient mean deviation, the coefficient of variation etc.
[next page]
|