1. It is rigidly defined. Its value is always definite.

2. It is easy to calculate and easy to understand. Hence it is very popular.

3. It is based on all the observations; so that it becomes a good representative.

4. It can be easily used for comparison.

5. It is capable of further algebraic treatment such as finding the sum of the values of the observations, if the mean and the total number of the observations are given; finding the combined arithmetic mean when different groups are given etc.

6. It is not affected much by sampling fluctuations.

Demerits

1. It is affected by outliers or extreme values. For example, the average (A.) mean of 10, 15, 25 and 500 is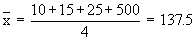

   Now observe first three values whose A.mean is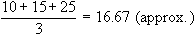

   Due to the outlier 500 the A. mean of the four numbers is raised to 137.5. In such a case A. mean is not a good representative of the given data.

2. It is a value which may not be present in the given data.

3. Many a times it gives absurd results like 4.4 children per family.

4. It is not possible to take out the averages of ratios and percentages.

5. We cannot calculate it when open-end class intervals are present in the data.

Newspaper : Punch, Quoted by Moroney

|"The figure of 2.2 children per adult female was felt to be in some respect absurd and the Royal Commission suggested that the middle class is paid money to increase the average to a rounder and more convenient number."

Index

4.1 Introduction
4.2 Arithmetic Mean
4.3 Properties of Arithmetic Mean
4.4 Median
4.5 Mode
4.6 Empirical relation between mean, median & mode

Chapter 5