Therefore, the median = 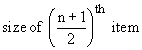
= 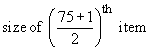
= size of 38th item
In the order of the cumulative frequency, the 38th term is present in the 50th cumulative frequency, whose size is 14.
Therefore, the median = 14
Median In Continuous Series (grouped Data)
Steps :
Determine the particular class in which the value of the median lies. Use 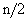 as the rank of the median and not as the rank of the median and not 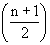
-
After ascertaining the class in which median lies, the following formula is used for determining the exact value of the median.
Median = 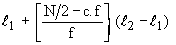
where,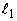 = lower limit of the median class, the class in which the middle item of the distribution lies. = lower limit of the median class, the class in which the middle item of the distribution lies.
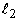 = upper limit of the median class = upper limit of the median class
c.f = cumulative frequency of the class preceding the median class
f = sample frequency of the median class
It should be noted that while interpolating the median value of frequency distribution it is assumed that the variable is continuous and that there is an orderly and even distribution of items within each class.
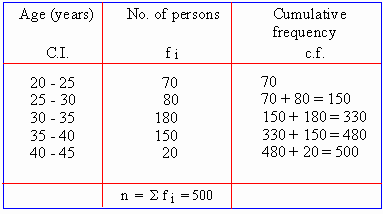
Example Calculate the median for the following and
verify it graphically.
Age (years) : 20-25 25-30 30-35 35-40 40-45
No. of person : 70 80 180 150 20
Solution:
|