-
Find the difference D = R1 - R2
where R1 = Rank of x and R2 = Rank of y
Note that S D = 0 (always) -
Calculate D2 and then find S D2 -
Apply the formula.
¬ Note :
In some cases, there is a tie between two or more items. in such a case each items have ranks 4th and 5th respectively then they are given 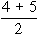 = 4.5th rank. If three items are of equal rank say 4th then they are given = 4.5th rank. If three items are of equal rank say 4th then they are given 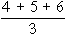 = 5th rank each. If m be the number of items of equal ranks, the factor = 5th rank each. If m be the number of items of equal ranks, the factor 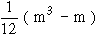 is added to S D2. If there are more than one of such cases then this factor added as many times as the number of such cases, then is added to S D2. If there are more than one of such cases then this factor added as many times as the number of such cases, then
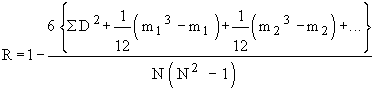
Example Calculate ‘ R ’ from the following data.
|
Student No.:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
|
Rank in Maths :
|
1
|
3
|
7
|
5
|
4
|
6
|
2
|
10
|
9
|
8
|
|
Rank in Stats:
|
3
|
1
|
4
|
5
|
6
|
9
|
7
|
8
|
10
|
2
|
Solution :
|
Student
No.
|
Rank in
Maths (R1)
|
Rank in
Stats (R2)
|
R1 - R2
D
|
(R1 - R2 )2
D2
|
|
1
|
1
|
3
|
-2
|
4
|
|
2
|
3
|
1
|
2
|
4
|
|
3
|
7
|
4
|
3
|
9
|
|
4
|
5
|
5
|
0
|
0
|
|
5
|
4
|
6
|
-2
|
4
|
|
6
|
6
|
9
|
-3
|
9
|
|
7
|
2
|
7
|
-5
|
25
|
|
8
|
10
|
8
|
2
|
4
|
|
9
|
9
|
10
|
-1
|
1
|
|
10
|
8
|
2
|
6
|
36
|
|
N = 10
|
|
|
S D = 0
|
S D2 = 96
|
Calculation of R :
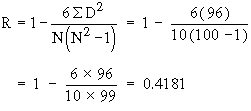
|
Index
6. 1 Introduction
6. 2 Correlation
6. 3 Types of Correlation
6. 4 Degrees of Correlation
6. 5 Methods of determining correlation
6. 6 Coefficients of Correlation for Bivariate
Grouped Data
6. 7 Probable Error
6. 8 Rank Correlation Coefficient
6. 9 Linear Regression
Chapter 7
|