|
2. Van Mise’s Statistical (or Empirical) Definition
If trials are to be repeated a great number of times under essentially the same condition then the limit of the ratio of the number of times that an event happens to the total number of trials, as the number of trials increases indefinitely is called the probability of the happening of the event.
It is assumed that the limit exists and finite uniquely. Symbolically p (A) = p = 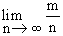 provided it is finite and unique. provided it is finite and unique.
The two definitions are apparently different but both of them can be reconciled the same sense.
Example Find the probability of getting
heads in tossing a coin.
Solution : Experiment : Tossing a coin
Sample space : S = { H, T} Þ
n (S) = 2
Event A : getting heads
\ A
= { H} Þ n (A) = 1
Therefore, p (A) = 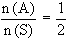 or 0.5 or 0.5
Example Find the probability of getting
3 or 5 in throwing a die.
Solution : Experiment : Throwing a dice
Sample space : S = {1, 2, 3, 4, 5, 6 }
Þ n (S) = 2
Event A : getting 3 or 6
A = {3, 6} Þ
n (A) = 2
Therefore, p (A) = 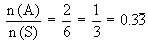
Example Two dice are rolled. Find the
probability that the score on the second die is greater than the
score on the first die.
Solution : Experiment : Two dice are
rolled
Sample space : S = {(1, 1), (1, 2), (1, 3), (1, 4), (1, 5), (1, 6) (2, 1), (2, 2), (2, 3), (2, 4), (2, 6)}...
(6, 1), (6, 2) (, 3), (6, 4), (6, 5), (6, 6) }
n (S) = 6 ´
6 = 36
[next page]
|