|
7.7 Theoretical Distributions
Random variable and probability distributions
Random variables : When we assign a number
to each point of a sample space, we have a function which is defined
on the sample space. This function is called a random variable (or
stochastic variable).
It is usually denoted by bold letters like X or Y.
Consider two independent tosses of a fair coin
\ S = { (HH), (HT), (TH), (TT) }
Let X denote the number of heads.
Then X (HH) = 2, X (HT) = 1, X(TH) = 1 and X(TT) = 0
i.e. X = 0, 1, 2. Here X is known as a random variable. Thus a random variable is one, which denotes the numerical value of an outcome, of a random experiment.
(1) If the random variable X takes only finite values or countably infinite values, then X is known as a ‘discrete variable’
(2) If the random variable takes the uncountably infinite
values between a specified range or limit, it is called as ‘continuous
random variable’.
For example : X denotes the age of a person.
Discrete probability distribution
Return to the above given example of tossing of a fair coin twice.
S = { (HH), (HT), (TH), (TT) }
Then X (HH) = 2, X (HT) = 1, X (TH) = 1 and X(TT) = 0
Also P (HH) = 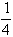 , P (HT) = , P (HT) =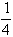 , P (TH) = , P (TH) = 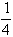 and P (HH) = and P (HH) = 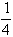
The probability distribution :- Number of Heads
X P(x)
0 ® 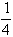 or
0.25 or
0.25
1 ® 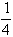 +
+ 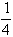 =
= 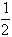 or 0.50
or 0.50
2 ® 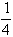 or
0.25 or
0.25
[next page]
|