|
7.8 Binomial Distribution
Bernoulliís trials : A series of independent
trials which can be resulted in one of the two mutually exclusive
possibilities 'successes' or 'failures' such that the probability
of the success (or failures) in each trials is constant, then such
repeated independent trials are called as "Bernoulliís trials".
A discrete variable which can results in only one of the two outcomes (success or failure) is called Binomial.
For example, a coin flip, the result of an examination success or failures, the result of a game - win or loss etc. The Binomial distribution is also known as Bernoulliís distribution, which expresses probabilities of events of dichotomous nature in repeated trials.
When do we get a Binomial distribution ?
The following are the conditions in which probabilities are given by binomial distribution.
- A trial is repeated 'n' times where n is finite and all
'n' trials are identical.
- Each trial (or you can call it an event) results in only
two mutually exclusive, exhaustive but not necessarily equally
likely possibilities, success or failure.
- The probability of a "success" outcome is equal
to some percentage which is identified as proportion, p
(or p)
- This proportion p (or p), remains
constant throughout all events (or trials). It is defined as the
ratio of the number of successes to the number of trials.
- The events (or trials) are independent.
- If probability of success is p or p,
then the probability of failures is 1 - p or 1 - p
this is denoted by q. Thus p + q = 1.
Suppose a coin is flipped twice. Let p (or p
) be the probability of getting heads and q the probability of tails,
such that p + q = 1 (note that p = q = 1/2 if the coin is fair)
Then there are three possible outcomes which are given below.
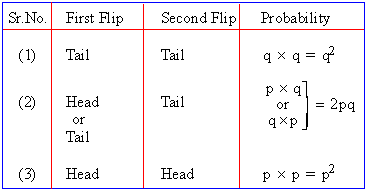
The sum of all these probabilities is q2
+ 2 pq + p2
= (q + p)2.
The terms of (q + p)2
in its expansion give the probabilities of getting 0, 1, 2 heads.
The result obtained above can be generalized to find the probability of getting 'r' heads in flipping n coins simultaneously.
The probabilities of getting 0, 1, 2, 3, .....,
r, .....n heads in a flip of 'n' coins are the terms of the expansion
(q + p)n. Since
the expansion is given by the Binomial Theorem, the distribution
is called Binomial Distribution.
Thus the Binomial formula is,
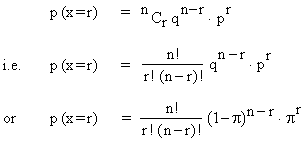
where n ! = n (n - 1) (n -2) .............3 . 2. 1
Properties of the Binomial distribution :
We get below some important properties of the Binomial distribution
without derivations.
- If x denotes the Binomial variate, expression of x i.e.
the mean of the distribution is given by,
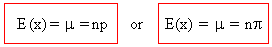
- The standard deviation of the Binomial distribution is
determined by,
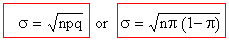
- If in experiment, each of n trials, is repeated N times
then expression of r successes i.e. the expected frequency of
r successes in N experiment is given by,
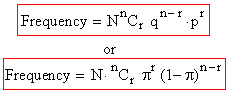
Example What is the expression of
heads if an unbiased coin is tossed 12 times.
Solution : Since the expression of
x in a binomial distribution is given by,
E (x) = np where n = 12 and p = 0.5 .
We could expect 12 ī 0.5
= 6 heads.
Example For a Binomial distribution,
mean is 2 and standard deviation is 1. Find all the constants of
the distribution.
Solution : We are given, Mean (m)
= n p = 2 and S.D. =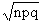
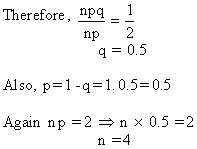
Hence the constants of the distribution are n = 4, p = 0.5 and q = 0.5
Example If the probability of a
defective bulb is 0.4. Find the mean and the standard deviation
for the distribution of the defective bulbs in a lot of 1000 bulbs.
What is the expected number of defective bulbs in the lot ?
Solution :
We have p = 0.4, n = 1000 and q = 1 - p = 1 - 0.4 = 0.6
Mean (m)
= np = 1000 ī 0.2 = 200
[next page]
|