| 7.6 Conditional Probability
In many situations you get more information than simply the total outcomes
and favorable outcomes you already have and, hence you are in position
to make yourself more informed to make judgements regarding the probabilities
of such situations. For example, suppose a card is drawn at random from
a deck of 52 cards. Let B denotes the event ‘the card is a diamond’ and
A denotes the event ‘the card is red’. We may then consider the following
probabilities.

Since there are 26 red cards of which 13 are
diamonds, the probability that the card is diamond is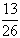 . In other words the probability of event B knowing that A has occurred
is
. In other words the probability of event B knowing that A has occurred
is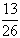 . .
The probability of B under the condition that
A has occurred is known as condition probability and it is denoted by P
(B/A) . Thus P (B/A) =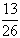 . It should be observed that the probability of the event B is increased
due to the additional information that the event A has occurred.
. It should be observed that the probability of the event B is increased
due to the additional information that the event A has occurred.
Conditional probability found using
the formula P (B/A) =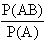
Justification :- P (A/B) =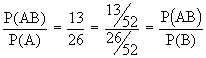
Similarly P(A/B) =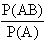
In both the cases if A and B are independent
events then P (A/B) = P (A) and P(B/A) = P(B)
Therefore P(A) = 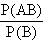 Þ
P (AB) = P (A) . P (B) Þ
P (AB) = P (A) . P (B)
or P(B) = 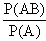 Þ
P (AB) = P(A) . P (B) Þ
P (AB) = P(A) . P (B)
Propositions
(1) If A and B are independent events then A
and B' are also independent where B' is the complementary event B.
(2) If A and B are independent events then A'
and B' are also independent events.
(3) Two independent events cannot be mutually
exclusive.
(4) De Morgan’s Laws : P (A È
B)' = P (A' Ç
B')
P (A Ç
B)' = P (A' È
B' )
Example A bag contains 6 red and 4 blue
balls. One ball is drawn at random from the first bag and put into the
second bag. A ball is then drawn from the second bag. What is the probability
that is red ?
Solution :
Let A = getting a red ball from the 1st bag.
B = getting a blue from the first bag.
C = getting a red ball from the second bag after
the ball drawn from the first bag is put into it .
[next page]
|