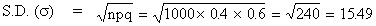
Expected number = n p = 0.4
´ 1000 = 400
Example Six dice are thrown 729
times. How many times do you expect at least three dice to show
5 or 6?
Solution : Let P = probability (showing 5
or 6) = 2/6 = 1/3
q = 1 - p = 1- 1/3 = 2/3
n = 6 and r = 3
Also p (x = r) = probability (at least 3 dice will show 5 or 6 in one trial)
Using the 'complement' theorem
p (x = r) = 1 - [p (x = 0) + p (x = 1) + p (x = 2)]
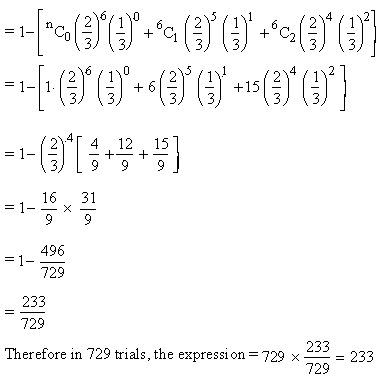
Therefore in 729 trials, the expression =
Example Take 100 sets of tosses of
10 flips of a fair coin. In how many cases do you expect to get
7 heads at least ? Solution : We have N = 100 sets. n = 10 trials in
each set p = 0.5 and q = 1 - p =0.5
Probability (getting at least 7 heads) in one set
= p (x = 7) + p (x = 8) + p (x = 9) + p (x = 10)
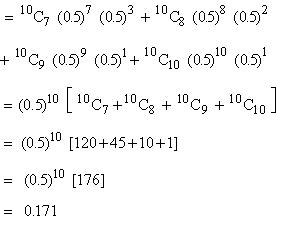
Therefore
in 100 sets = N p (r) = 100 ´
(0.171) @ 17 times you
can expect to get at least 7 heads.
Example If the probability of success
is 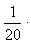 How
many trials are required in order that the probability of getting
at least one success, is just greater than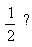 
Solution :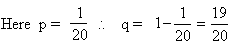 
Let 'n' be the required number of trials
to get the probability of at least one success which
is ,
1 - n C 0 P 0
Q n-0 \
[ since probability (at least one success) = 1 - p (x = 0)
i.e. 1 - probability (No success)]
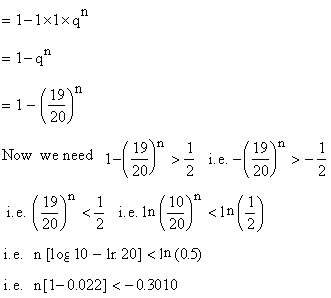
[next page]
|
