|
7.4 Definitions of Probability
We shall now consider two definitions of probability :
(1) Mathematical or a priori or classical.
(2) Statistical or empirical.
1. Mathematical (or A Priori or Classic) Definition
If there are ‘n’ exhaustive, mutually exclusive and equally likely cases and m of them are favorable to an event A, the probability of A happening is defined as the ratio m/n
Expressed as a formula :- 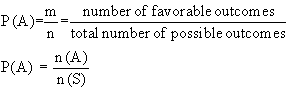
This definition is due to ‘Laplace.’ Thus probability is a concept which measures numerically the degree of certainty or uncertainty of the occurrence of an event.
For example, the probability of randomly drawing taking from a well-shuffled deck of cards is 4/52. Since 4 is the number of favorable outcomes (i.e. 4 kings of diamond, spade, club and heart) and 52 is the number of total outcomes (the number of cards in a deck).
If A is any event of sample
space having probability P, then clearly, P is a positive number
(expressed as a fraction or usually as a decimal) not greater than
unity. 0 £
P £ 1 i.e. 0 (no chance or for
impossible event) to a high of 1 (certainty). Since the number of
cases not favorable to A are (n - m), the probability q that event
A will not happen is, 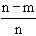 q = or q = 1 - m/n or q = 1 - p.
q = or q = 1 - m/n or q = 1 - p.
Now note that the probability q is nothing but the probability of the complementary event A i.e. 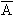
Thus p (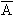 ) = 1 - p or p ( ) = 1 - p or p (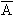 ) = 1 - p ( ) = 1 - p (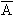 ) )
so that p (A) + p (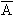 )
= 1 i.e. p + q = 1 )
= 1 i.e. p + q = 1
Relative Frequency Definition
The classical definition of probability has a disadvantage i.e. the words ‘equally likely’ are vague. In fact, since these words seem to be synonymous with "equally probable". This definition is circular as it is defining (in terms) of itself. Therefore, the estimated or empirical probability of an event is taken as the relative frequency of the occurrence of the event when the number of observations is very large.
[next page]
|