|
Example Assume that the probability of
a bomb dropped from an aeroplane, striking a target is 1/5. If 6
bombs are dropped, find the probability that
(1) exactly two will strike.
(2) at least two strikes the target.
Solution :
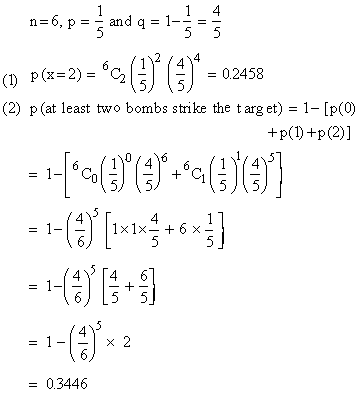
Example The probability of a man
hitting a target is 1/3. How many must he fire so that the probability
of hitting the target, at least once, is more than 90% ?
Solution : Here p = 1/3 and q = 2/3
and n = ?
Now, p (hitting the target at least once) > 90%
p ( x
³ 1) = 1 - p (x
= 0) must be greater than 90%
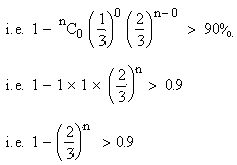
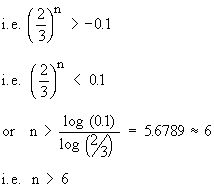
Therefore, he must fire at least 6 times so that
the probability of hitting the target at least
once is more than 90%
Example If an average 8 ships out
of 10 trials arrive safely at a port. Find the mean and standard
deviation of the number of ships arriving safely out of the total
of 1600 ships.
Solution : p = 0.8 therefore q = 1 - p = 1- 0.8 =
0.2 and n = 1600
Mean (m) = n p = 1600
´ 0.8 = 1280
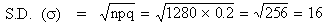
Hence the mean and standard deviation of ships, returning safely
respectively 1280 and 16.
Example In a hurdle race, a player
has to cross 10 hurdles. The probability that he will clear each
hurdle is 5/6. What is the probability that he will knock down fewer
than 2 hurdles ?
Solution : n = 10, q = probability that
he will clear each hurdle = 5/6
p = probability that he will knock down
= 1 - 5/6 = 1/6
Therefore, p (knocking down fewer than 2 hurdles) = p (0) + p (1)
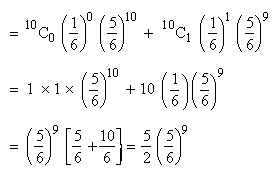
[next page]
|