7. The angles of a quadrilateral are in the ratio 2 : 3 : 5 : 8. Find them in degree as well as in radians.

Solution

Let the angles be 2k, 3k, 5k and 8k in degrees.
For a quadrilateral, 2k + 3k + 5k + 8k = 360⁰

\ 18k = 360⁰ \ k = 20⁰

\ The angles are 2k = 40⁰ , 3k = 60⁰ , 5k = 100⁰
and 8k = 160⁰

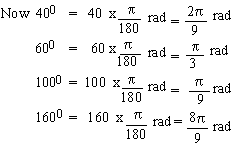
8. The angles of a triangle are in A.P. such that the greatest is five times the least. Find the angles in degrees and radians.

Solution

Let the angles of a triangle in A.P. be,
a - d, a and a + d respectively
\ (a - d) + a + (a + d) = 180⁰ \ 3a = 180⁰\ a = 60⁰
\ The greatest angle be (60 +d)⁰ and the least angle be
(60 - d)⁰

Given that (60 + d) = 5 (60 - d)

\ 60 + d = 300 - 5d

\ 6d = 240 \ d = 40⁰

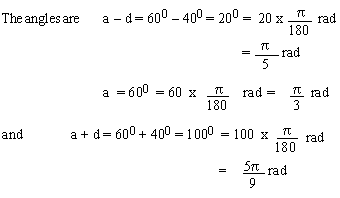
9. The length of an arc of a circle is 7 cm. Find the angle (in degrees and radians) it makes at the centre, if the radius is 4 cm. Give the answer to three significant digit.

Solution

Given that s = 7cm , r = 4 cm with usual notations.

Now we have s = r q^c \ q = 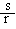= 7 cm = 1.75 rad

10. If D, G, C are respectively the numbers in degrees, grades and radians of an angle. Show that

(i) 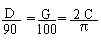(ii)

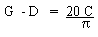
Solution

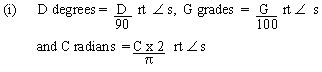
Index

1.1 Angles (Radians & Degrees)
1.2 Arc Length & Area of the circle
Supplementary Problems

Chapter 2