|
CHAPTER 3 : TRIGONOMETRY OF TRIANGLES
Every triangle has six measurements which are also
known as six elements of a triangle. They are three sides and three
angles.
Note that lower case letters such as a, b, c....
are used to denote the length of sides (or to name the sides) of
a triangle that are opposite the anlges named with corresponding
upper-case letters Ð A, Ð
B, Ð C ..... resp.
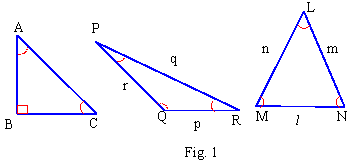
Generally when any three elements are given, the
remaining three elements can be found out (except the case when
only the three angles are given; for in this case we do not get
the definite values of sides).
Solution of a triangle : The process of finding
out the other elements of a triangle when any three elements are
given (except the case of three angles) is called the solution of
the triangle.
3.1 Solving Right Triangles
Cases : When given
(I) Hypotenuse and one side.
(II) Two sides other than hypotenuse.
(III) One angle (other than right angle) and its opposite side.
(IV) One angle (other than right angle) and its adjacent side (other
than hypotenuse).
(V) One angle (other than right angle) and hypotenuse.
Clearly speaking still many cases exist. But for a right triangle
all these are easy !
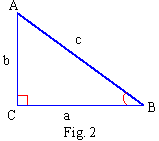
(I) Hypotenuse and one side : Let 'b' and hypotenuse
'c' be given. Solving the right triangle as a2 = c2
- b2 . Hence 'a' is known. Consider sin B = b / c using
calculator or table Ð B can be
known. Also Ð A = 90 - m
Ð B \ Ð A is known.
Now here all the sides and angles are known, hence
the triangle is solved.
[next page]
|