| 2.4 Tables of Trigonometric Function
When solving problems using trigonometric functions,
either the angle is given and the value of t-function must be found,
or the value of the t-function is given and angle must be found.
These two processes are inverse of each other.
Thus inverse notations are used to express an angel in terms of
the values of t-functions. For instant cos
a = 0.5 can be put in the form a = cos -1 (-0.5)
or a = Arc cos (- 0.5). The two expressions
are read as Alpha equals to 'Inverse cos of (-0.5) or Alpha equals
to Arc cos (- 0.5).
Both these operations can be done either using
a calculator or using a trigonometric table. It should clearly be
noted that both calculator or a table gives only approximate answers.
Even so we use equality sign (=) but more correctly the use of approximation
sign ( » ) is welcomed. Approximate
values of the functions of acute angles are given in Tables of
Natural Trigonometric functions. We shall use a Trigonometric
table giving values to four decimal places. As it is clear that
Tables cannot list all angles. Therefore, approximation must be
used to find values between those given in the table. This method
is known as Linear interpolation.
Assumption :
Differences in functional values are directly proportional to the
Differences in measures of angle over a very small interval.
Caution : This is not a real
truth ! Yet it gives a better answer than just going for nearest
value in the table.
Illustration 1
Using linear interpolation Find sin (240
43'), given that sin (240 40') = 0.4173 and sin (240
50') = 0.4200
Solution
We have sin (240 50') = 0.4200
and sin (24 0 40')= 0.4173
Difference for 10'= 0.0027
Owing to the assumption made if x is the difference
for required 3' we have a ratio
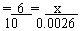
\ x = 0.3 (0.0027)
= 0.00081 » 0.0008 (rounded off to 4 decimal places)
Thus sin (240 40') = sin (24040') + sin (0.3')
angle increase with an increment in its sine of angle and vice versa.
Thus sin (240 43') = 0.4173 + 0.0008 = 0. 4181
Illustration 2
Find cos (640 26'), given that cos (640
20') = 0.4331 and cos (640 30') = 0.4305
Solution
We have cos (640 30') = 0.4331
cos (640 20') = 0.4305
\ Tabular difference
for 10' = 0.0026
\ The required difference
for 6' =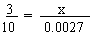 (If x)
(If x)
\ x = 0.6 (0.0026) =
0.00156 or 0.0016 (104 decimal places)
As the angle increases, the cosine of angle decreases.
Thus cos (640 26') = 0.4331 - 0.0016
= 0.4315.
Illustration 3
Find tan (28.43)0, given that tan (28.40)0
= 0.5407 and tan (28.50)0 = 0.5430
Solution
= 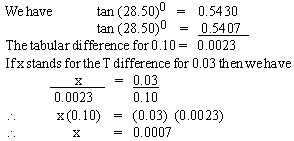
As angle increases, the tangent of angle also
increases.
Thus tan (28.43)0 = 0.5407 + 0.0007 = 0.5414
Illustration 4
Solve the right triangle in which a = 24.36
Ð A = 58053'.
Solution
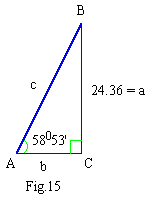
In right triangle ABC
A + B + C = 1800
\ 58053' + B + C = 180
0, given that C = 900
\ B = 90 0 - 58053'
= 310 7'
Using the formulas for t-ratios,
b / a = cot A, b = a cot A = 24.36 (0.6036) = 14.70 (\
cot A = 0.6036)
c/a = csc A, c = a csc A = 24.36 (1.1681) = 28.45
a/c = sin A, c = a / sin A = 24.36 / 0.8562 = 28.45
b/c = cos A, b = c cos A = 28.45 (0.5168) = 14.70
Note : To save time, consider
Illustration 1
Step (1) sin (240 41') = 0.4173, take only 4173
(2) Find mentally the tabular difference 27 between 4200 (for sin
240 40') and 4173 (for sin 240 40')
(3) Difference for 3' = 0.3 (27) = 8.1 (rounded off).
(4) Add (since sine) to 4178 to get 4181 then sin 240
31' = 0.4181.
Illustration 5
Find angle A, given that sin A = 0.4234
Solution
We will not find this entry in the table.
However 0.4226 = sin 250 0'
0.4253 = sin 250 10'
Tabular difference = 0.0027
Now 0.4226 = sin 25.0'
0.4234 = sin A
0.0008 = partial difference
correction =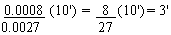 (nearest minute)
(nearest minute)
Adding (since sine) the correction is A = 250 0' + 3'
= 250 3'
Illustration 6
Find A, given that cot A = 0.6345
Solution
We have 0.6330 = cot 570 40' (from the table)
0.6371 = cot 570 30'
Tabular diff. = 0.0041
Now 0.6330 = cot 570 40'
0.6345 = cot A
Partial diff. = 0.0015
Correction = 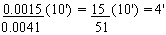 (nearest minute)
(nearest minute)
subtracting (since cot), the correction is A = 570 40'
- 4' = 570 36'.
Note : Saving the time as
- (Consider Illustration 5)
Step (1) Locate the next smaller entry, 0.4226 = sin 250
0'. Use 4226 only.
(2) Find tabular diff. (mentally), 27.
(3) Find partial diff. (mentally), 8 between 4226 and 4234.
(4) Find 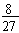 (10') = 3' and add (since sine) to get A = 250 3'
(10') = 3' and add (since sine) to get A = 250 3'
Commit to memory the values of t-functions of angles measuring 00,
300 , 450, 600 and 90 0as
follows:
(1) Write angle (q) in the given order
in the 1st column and the t-ratios, sin q,
cos q, tan q,
csc q, sec q,
cot q in the 1st row.
(2) Put 0, 1, 2, 3, 4 in sin q column
(see the table), then put 4, 3, 2, 1, 0 in cos q
column (see the table).
(3) Divide by 4 to each entry then find square root of each entry.
These are values of sine and cosine ratios of angles 00,
300, 450, 60 0and 900
(4) Use tan q = 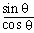 q and reciprocal relations for csc q,
sec q and cot q.
q and reciprocal relations for csc q,
sec q and cot q.
Thus we have

Click here to enlarge
Note that
- As the measure of the angle increases values of sine ratios
increases till 900 (p /
2 rad) and then decreases.
- As the measure of the angle increases values of cosine ratios
decreases till 900 (p /
2 rad) and then increases.
- As the measure of the angle increases values of tangent ratio
increases indefinitely till 900 (p
/ 2 rad), then decreases indefinitely.
Also note that
- Since sin2q + cos2q
=1 we have | sin q | £
1 i.e. - 1 £ sin q
£ 1 and |cos q
| £ 1 i.e. - 1 £
cos q £
1 for all q . These are called bounds
of sine and cosine ratios.
- Since csc q =
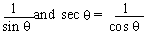 we have,
we have,
csc q ³
1 or csc q £
1 and sec q
³ 1 or sec q
£ 1 (numerically) for admissible values of q
.
- tan q and cot q
can take all real values of q .
|