|
2.2 Fundamental Relations between the trigonometic ratios of
an angle
 
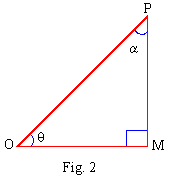 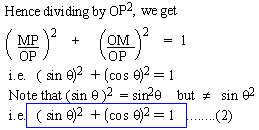 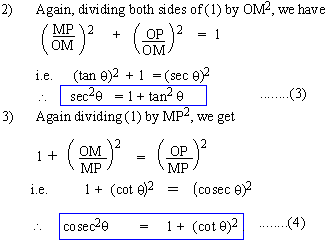
From (3) we have, sec2q -
tan2q = 1 and
From (4) we have, cosec2q
- cot2q = 1
Trigonometric Functions Of Complementary Angles
let Ð OPM = a
so that (q + a)
= 900 \ a
= (90 - q)
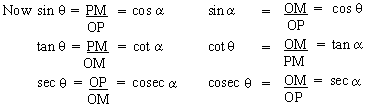
Here q and a
are measures of complementary angles
Thus, in general :
sin q = cos (90 - q)
cos q = sin (90 - q)
tan q = cot (90 - q)
cot q = tan (90 - q)
sec q = cosec (90 - q)
cosec q = sec (90 - q)
These relations, associates the functions in pair
- (sine and cosine), (tangent and cotangent) and (secant and cosecant).
These three pairs of trigonometric functions are called "Cofunctions"
|