Given that : AC = 6 ft. BD = 1 ft.
and cos C = 0.9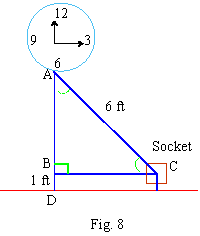
Now    cos C² = 1 - sin²C
or        sin²C   =   1 - cos²C

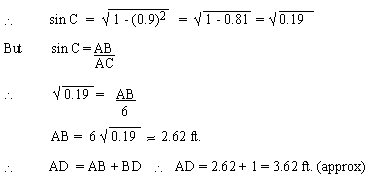
6. Find q in fig. without using trigonometric table or a calculator to find the value of t- functions.

Solution

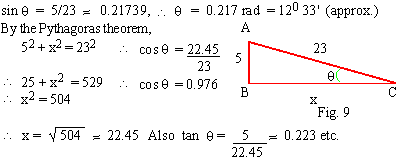
7. A ladder leans against the side of a building with its foot 12 ft from the building. How far from the ground is the top of the ladder and how long is the ladder if it makes an angle of 70⁰ with the ground ?

Solution

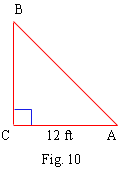From fig., tan A = CB / AC \ CB = AC tan A
\ CB = 12 tan 70 ⁰ = 12 (2.7) = 32.4
The top of the ladder is 32.4 ft. above the ground. sec A = AB / AC ; then AB = AC sec A = 12 (2.9) = 34.8 \ The ladder is 34.8 ft. long.

Angles In Standard Positions

1. With respect to a coordinate system, an angle is said to be in "standard position" when its vertex is at the origin of this rectangular coordinate system and its initial side coincides with the positive of x-axis.

2. When the terminal side of an angle in standard position falls in any quadrant, then the angle is said to be "angle of that quadrant."

   
   [next page]

Index

2.1 Trigonometric Ratio of Acute Angles
2.2 Fundamental Relation between the trigonometric Ratios of an angle
2.3 Functions of General Angles or t Ratio
2.4 Tables of Trigonometric Function
Supplementary Problems

Chapter 3