|
Example 5
One side of a triangle of length 20, forms a 420 angle with a second side.
The length of the third side is 14. Find the length of the second side.
Solution
Let the required triangle be ABC. Given that a = 20, b = 14, and Ð B
= 420

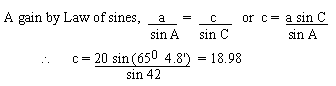
\ The first solution of D
ABC is obtained.
The second solution will be obtained as
Let – A' , – B and – C' and a' , b' and c' be the elements of the second solution. Let this triangle be A'BC'
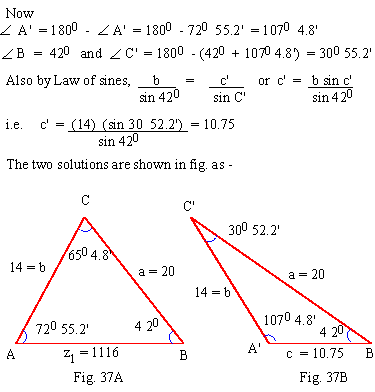
[next page]
|
Index
3. 1 Solving Right Triangles
3. 2 Law of Cosines
3. 3 Law of Sines
3. 4 The Ambiguous Case of Law of Sines
3. 5 Areas of Triangles
Supplementary Problems
Chapter 4
|