|
3.3 Law Of Sines
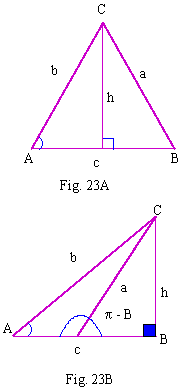
In triangle ABC, seg 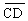 is
the altitude in each fig. is
the altitude in each fig.
\ D ADC and D
BCD are right triangles. Thus
sin A = 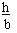 \ h = b sin A in fig.23A
\ h = b sin A in fig.23A
sin ( p - B) = sin B = 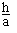 \ h = a sin B.
\ h = a sin B.
In follows that from fig.23.B
\ b sin A = h = a sin B
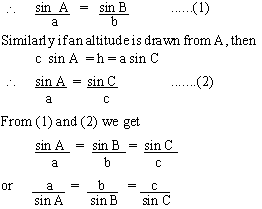 
The Law Of Tangent
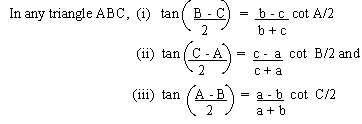
These results are also known as "Napier's Analogy."
[next page]
|