|
SUPPLEMENTARY PROBLEMS
1. (a) Solve the following oblique triangle ABC, given
a = 125, Ð A = 540
40' , Ð B = 650 10'
Answer :- b = 139, c = 133, Ð
C = 600 10'
(b) a = 320, c = 475, A = 350 20'
Answer :- b = 552, Ð B = 850
30', Ð C = 590 10'
b' = 224, Ð B' = 230
50', Ð C' = 1200 50'
(c) Solve the triangle whose sides are respectively 52.8, 39.3
and 72.1
Answer :- Ð A = 450
44' , Ð B = 320 12',
Ð C = 1020 4'
(d) In triangle ABC, a = 54 cms, b = 78 cms and c = 92 cm. Find
the greatest angle.
(e) The sides of the triangle are 7 cms, 4 Ö
3 cms and Ö 13 cms. Find
the smallest angles.
2. (a) A light house is 10 miles northwest of a dock. A
ship leaves the dock at 9 A.M. and steams west at 12 miles / hour.
At what time will it be 8 miles from the light house ?
(b) Two forces of 115 1b and 215 1b acting on an object have a
resultant of magnitude 275 1b. Find the angle between the directions
in which the given forces act .
Answer : - 700 50'
(c)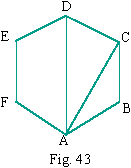 
In the regular hexagon shown. Find the length AC and AD if each
side has length 6.23 units. Use the fact that in a regular hexagon,
each angle is,
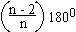
Answer : AC = 10.7907, AD = 12.4600
(d) Two planes take off from the same air port. The first one
flies on a course of 220.10. The second one flies on
a course of 154.40. After the first plane flies 362.4
kms, the course from the second plane is 83.50. How far
is the second plane from the airport ?
Answer : 263.507 kms.
3. (a) Verify the identity (a - b) cos r /2 = c sin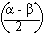 
, which is known as Mollweide's formula.
(b) Prove that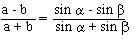 
4. (a) Solve the triangle ABC if a = 12, b = 10 and a
= 510
Answer :- b1 = 40.36 25
, b2 = 139.637 g1
= 88.6375, g2 =
-10.6370, c1 = 15.4367. Since negative angle g2
is impossible. There is only one solution. Check it by b < a.
(b) A small electronic component in the shape of a triangle with
sides 6.23, 8.146 and 11.392 millimeters. Find the largest angle.
Ans :- 104.031 0
**********
[next chapter]
|
