|
Example 12 Prove that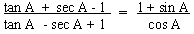 
Solution
Example 13
Verify that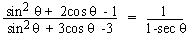 
Solution
Example 14 If x = r cos A cos
B, y= r cos A sin B and z = r sin A prove that X2 + Y2
+ z2 = r2
Solution
x2 + y2+ z2=
r2 ......(given to be proved.)
x2 + y2+ z2= r2
\ (r cos A cos B)2
+ (r cos A sin B)2+
(r sinA) 2 = r 2 ....substituting the given
relations.
\ r2cos2A
cos2 B + r2cos2 A sin2
B + r2sin2A = r2 ....(algebraic
manipulation)
\ r2cos 2
A (cos2B+ sin2B) + r2 sin2A
= r2 .....(combining terms)
\ r2cos2A
(1) + r2sin2 A = r 2 ....Pythagorean
identity
\ r2(cos2
A + sin2 A) = r2
\ r2(1) .....Pythagorean
identity.
Example 15
Solution
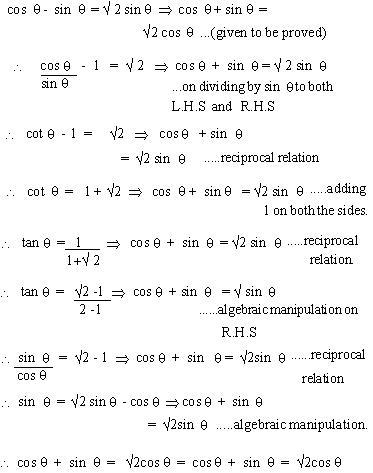
Example 16 Show that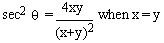 
Solution
We know that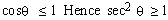 
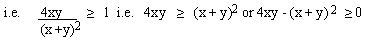
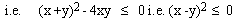
since (x-y)2is a complete square, it
can't be negative.
\ (x -y)2=
0 is the only possibility.
\ (x -y) = 0 i.e. x
= y.
Example 17 If a and b are two
positive real numbers. Can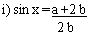 
ii) tan x = b/a? Give reasons.
Solution
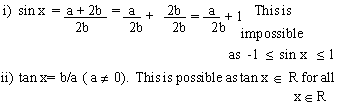
Example 18 Express each of
other trigonometric ratios of 
in terms of sin .
Solution
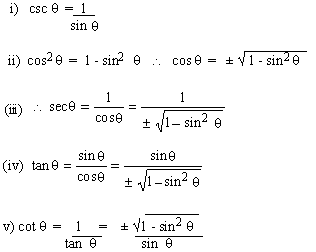
Example 19 If
is in Quadrant IV, express the other trigonometric functions of
in terms of sec .
Solution
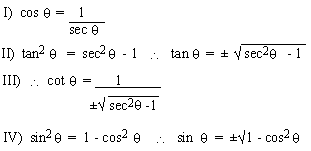
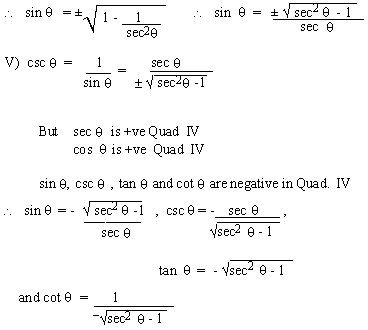
[next page]
|
