|
Example 6
Express in the form a + bi
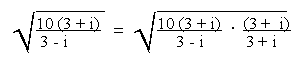
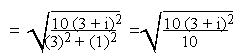 = (3 + i)
= (3 + i)
\ 3 + i
= a + bi where a =
3 and b = 1
b) 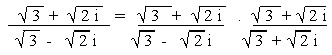
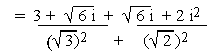
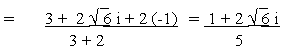
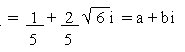
\
a = 1/5 and b = 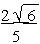
Example 7
If z1 = 6
- 2i and z2 = 2
- 5i find (a) | 2 z1- 3z2
|
Solution
2z1 - 3z2 = 2 (6 - 2i) - 3 ( 2 -5i) = (12
- 6) + (-4 + 15) i = 6 + 11i.
Now | 2z1 - 3z2 | = 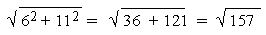
(b) | z1. z2|
Solution
z1 . z2
= (6 - 2i) (2 - 5i) = 12 - 30i - 4i
+ 10i2
= 12 - 34i - 10 = 2 - 34i \ |z1
. z2 |
= 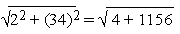
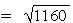
(c) 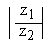
Solution
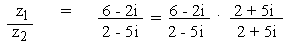
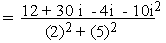
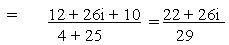 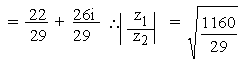
(d) 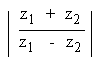
Solution
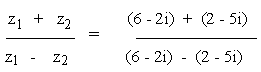
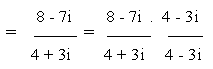
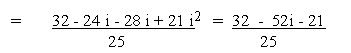
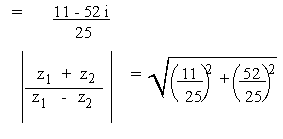
= 2.126 (approx.)
Example 8
Find arg (z) if (a) z = 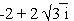
Solution
Let a + bi = 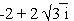
so that a = -2 and b = 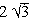
Now 
or 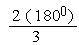 = 1200
= 1200
(b) z = 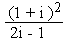
Solution
a + bi = 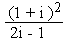
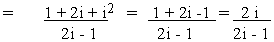
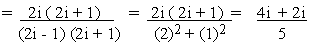
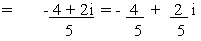
so that a = - 4/5 and b = 2 / 5 \
arg (z) = 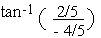
arg (z) = tan-1 (-1/2)
(c) If z1 = 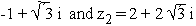 Find arg ( z1 . z2)
Find arg ( z1 . z2)
Solution
( z1 . z2) = 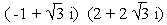 =
= 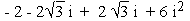 = -8 + 0i
= -8 + 0i
\ arg ( z1 . z2) = tan-1(0/-8)
= 0 or p
Example 9
Express in the form a + bi.
(a) 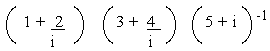
Solution
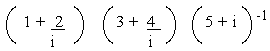
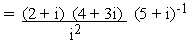
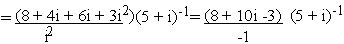
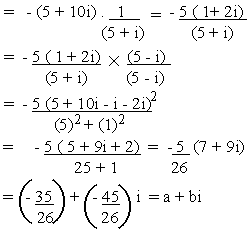
(b) 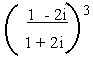
Solution
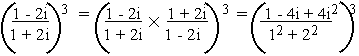
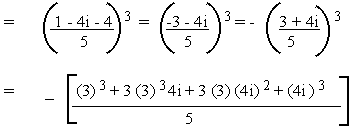
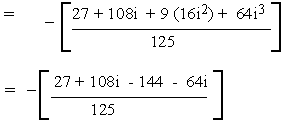
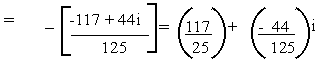
= a + bi
[next page]
|