|
8.3 Roots of Complex Numbers
Given a complex number z = r (cos q
+ i sin q) . All the roots of 'z' are
given by
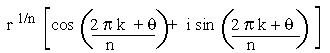
where k = 0, 1, 2, 3, ...., (n-1)
i) If k = 0 then 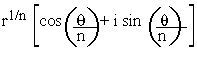 which is the principal nth root of z
which is the principal nth root of z
ii) Also, for q = 0 and r = 1 then z = 1 and nth root
of unity are given by
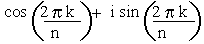 ,k = 0, 1, 2, 3, ...., (n - 1)
,k = 0, 1, 2, 3, ...., (n - 1)
Example 1
Find three cube roots of unity.
Solution
n = 3 (1)1/3 = 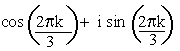
Thus z3 = 1 and k = 0, 1, 2
when k = 0 z1 = cos (0) + i sin (0)
z1 = 1
when k = 1, z1 = 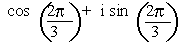
= cos (1200) + sin (1200)
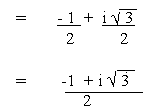
when k = 2 , z3 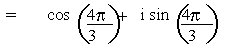
= cos (2400) + i
sin (2400)
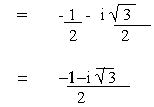
Hence the three cube roots of unity are 1, 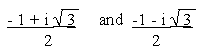
Note that these roots are also denoted by 1, w and w2 respectively
Also, not that they are in geometric progression and we have
l + w + w2 = 0, w3 = 1 etc.
Example 2
Prove that the nth roots of unity form a G.P and each can be shown
as power of the other.
Solution
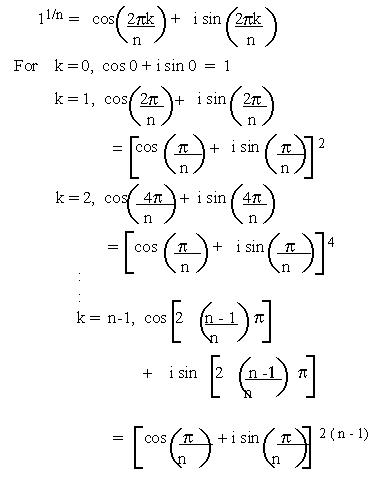
Let these roots be denoted by 1, w, w2......, wn
-1 forms a G. P. with common ratio
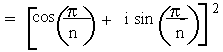
[next page]
|