8.4 Circular Functions of Complex angles & Hyperbolic Function

We have Eular's formulas, e^iq = cosq + i sin q ® (1)
            and e^-iq = cosq - i sin q ® (2)

          Þ e^iq + e^-iq= 2 cos q and e^iq - e^-iq = 2 i sin q

Whence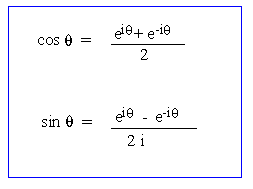

For any non-real quantity z, we have sinz =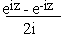

cos z = 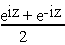tan z = 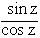with csc z, sec z, cot z as their respective reciprocals.

HYPERBOLIC FUNCTIONS

From the analogy, we define the new functions known as Hyperbolic functions

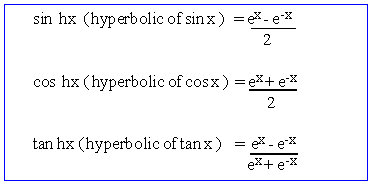
and csc hx, sec hx, cot hx are their reciprocals respectively.

Relation between circular and hyperbolic functions

We have sin q =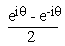

       \ sin(ix) =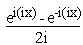

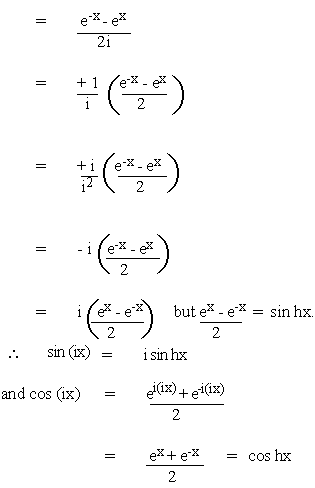
Hence we have

  (A)   sin (ix) = i sin hx         (B)  sin hix = i sin x

            cos (ix) = cos hx               cos hix = cos x

           tan (ix) = i tan hx              tan hix = i tan x

Note that - ¥ < sin hx < ¥, 1 £ cos hx £ ¥ and -1 £ tan hx £ 1

Observe the following table

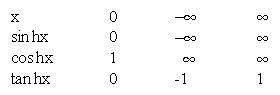
[next page]

Index

8.1 Geometry of complex numbers
8.2 De - Moivres's theorem
8.3 Roots of complex numbers
8.4 Cirsular functions of complex angles & hyperbolic function
Supplementary Problems

Chapter 9