|
Example 7
Find the continued product of all values of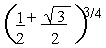 
Solution
1 +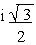 
= cos (2 p k + p
/ 3) + sin (2 p k + p
/ 3)
Note that r =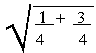 
= 1 and q = tan-1(Ö
3 / 2) = 600 or p/3c
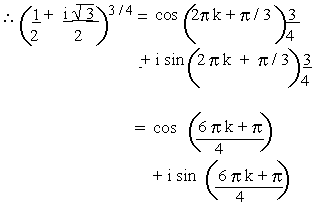
putting k = 0, 1, 2, 3, we get
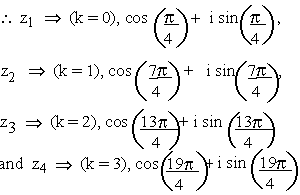
Therefore the continued product is
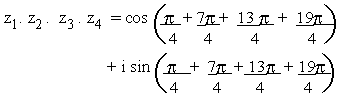
\ z1 . z2 . z3
. z4 = cos (10p) + i sin (10p)
= cos (0) + i sin (0) = 1 + i (0) = 1
Example 8
If l + 2i is one root of x4 - 3x3 + 8x2
- 7x +5 = 0. Find the other roots.
Solution
Let a = = 1 + 2i then b
= 1 -2i
We know that a quadratic equation in x, having roots a
and b, can be put in the form
x2 - ( a + b ) x + a . b = 0
\ x2 - [ (1 + 2i) + (1
- 2i) ] x + (1 + 2i) (1 - 2i) = 0
\ x2 - 2x + 5 = 0
Dividing by x2 - 2x + 5 = 0 to x4 - 3x3
+ 8x2 - 7x + 5 = 0 as
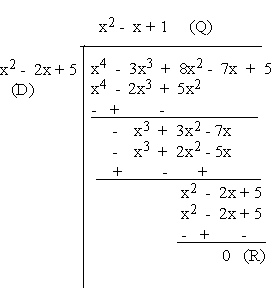
Since R = 0, x2 - x + 1 = 0 is the other factor of
the given expression.
Thus the other factor is x2 - x + 1 whose roots are
Now x =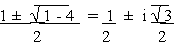 
Therefore x4 - 3x3 + 8x2 -
7x + 5 = 0 has roots
1 + 2i, 1 - 2i,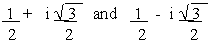
Example 9
Find two values of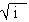 
Solution
i = cos 900 + i sin 900....[ since
cos 900 = 0 and sin 900 = 1]
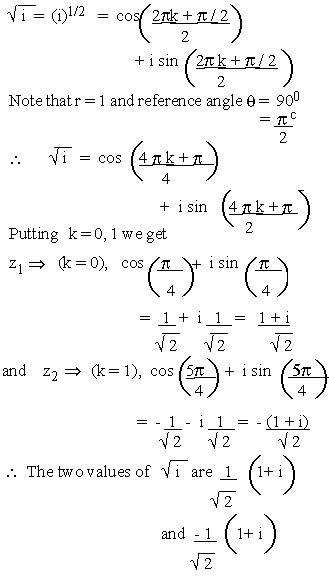
Example 10 Find the two values
of the sq.root of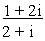 
Solution
1 + 2i Þ a = 1 > 0 and b =
2 > 0 i.e. (q is in 1st quad.)
\ r =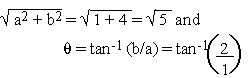 
= 63026'
Also, 2 + i Þ a = 2 > 0 and
b = 1 > 0 i.e. (q is in 1st quad.)
\ r = Ö4+1
= Ö5 and q
= tan-1(1/2) = 26034'
\ 
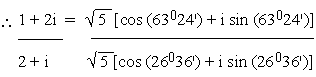
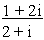= cos (63024' - 26036') + i sin
(63024' - 26036' )
= cos (36052') + i
sin (36052')
Now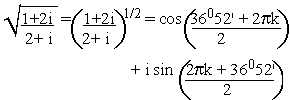 
= cos 36052' + 2pk + i
sin 2pk + 36052'
....... by using z1/n = r1/n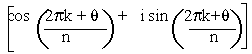
When k = 0
\ 
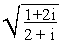= cos (18026') + i sin (18026') = 0.9487 +
0.3162i
When k = 1
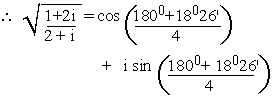
= cos (198026') + i sin (198026')
= - 0.9487 - 0.3162i
Thus required sq.roots are ± (0.9487 + 0.3162i)
Example 11 The centre of a regular hexagon is at the origin
and one vertex is given by (1+i) on the Argand's diagram. Find the
remaining vertices.
Solution
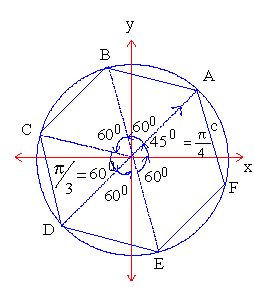
Since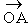 
represent Aº (1+ i) the first vertex
of the regular hexagon ABCDEF.
Now 1+ i Þ a=1 and b=1 (i.e. q
in 1st quad.). We have r=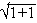
= 
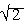units i.e. ||
=
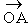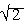units and q = tan-1(1/1) =
p/4 = 450. \
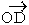makes 450 angle with 
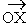and of length
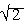units. Being regular hexagon  ,
 ,
,
 ,
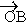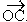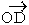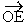q make angles of p/3,
2p/3, p, 4p/3,
5p/3 with .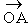
This shows that modulus of all these six vertices is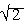
units and their respective amplitudes are, (p/4+
p/3), (p/4+2p/3),
(p/4+p), (p/4+5p/3)
for B, C, D, E and F.
\ Radius vectors representing the vertices
are
A,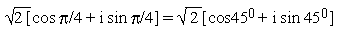 
B,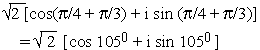 
C,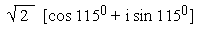 
D,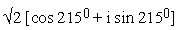 
E,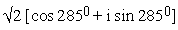 
and
F,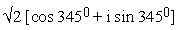 
i.e. A is (1+i), B is (-0.366 + 1.366i), C is (-1.366 + 0.366i),
D is (-1-i), E is (0.366 - 1.366i) and F is (1.366 - 0.366i) .
[next page]
|
