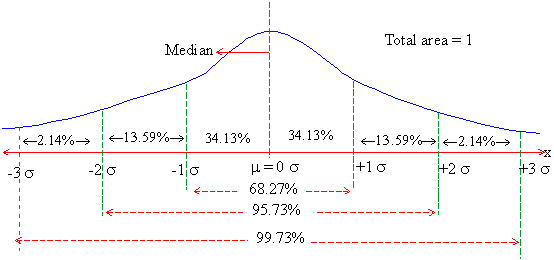
The area under the normal curve is distributed as follows :
1. The area between x = m - s and x = m + s is 18.27%
2. The area between x = m - 2s and x = m + 2 s is 95.45%
3. The area between x = m - 3 s and x = m + 3 s is 99.73%
These areas are shown in the following figure.
Click here to enlarge
i.e. P ( m - s < x < m + s ) = 68.27%
P ( m - 2s < x < m + 2s ) = 95.73%
P ( m - 3s < x < m + 3s ) = 99.73%
m ± 1s are points of inflexons
Example For a normal distribution the mean 50 and the standard deviation is 15. Find i) Q1 and Q3 ii) Mean deviation and also the interquartile range.
Solution : For a normal distribution
Q1 = m - 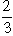 s = 50 - s = 50 - 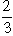 ´ 15 = 40 ´ 15 = 40
Also Q3 = m + 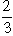 s - 50 + s - 50 + 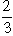 ´ 15 = 60 ´ 15 = 60 The mean deviation is = 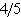 s = s = 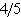 ´ 15 = 12 ´ 15 = 12 Inter quartile range = Q 3 - Q 1 = 60 - 40 = 20
The Standard Normal Variate ( Z-Score ) :
The problem of finding the probability reduces to finding the area
between the two ordinates. For different values of m
and s we get different normal curves,
which multiplies it into too many problems if we are to find the
area between the given values for different curves with different
m and s
.
All such problems can be reduced to a single one by reducing all normal distributions to a single normal distribution called 'Standardized Normal Distribution' or to what is known as the z-score.
To convert a value to a z-score is to express it in terms of how many standard deviations it is above or below the mean. This actually amounts to the shifting of the origin to m
and reducing its scale by s
.
Thus,
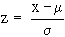
where x = the value to be converted, m
= the population mean and s
= the population standard deviation. obviously the m
= 0 and s
= 1 for the Normal standard distribution. it is denoted by N (0,1 ).
The areas under the curve between x = 0 and various ordinate x = a are in a table of standard normal probabilities. This area is equal to the probability that x will assume a value between x = 0 and x = a.
How to use Table : The table gives the areas from the ordinate x = 0 to x = 3.09 which covers more than 0.499 units of area on one side i.e. more than 0.99 units of area on both sides, the total area being 1, and it is 0.5 on both sides.
If the variate is not standardized first then convert it into
a standardized normal variate i.e. z-score, using z =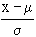 and find the limits of z-score corresponding to the given limits
of the variate.
and find the limits of z-score corresponding to the given limits
of the variate.
If we want to find the probability of x between x = a, and x = b, we find z from z = 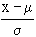
Suppose those values are a and b. Then referring to the table we find the area between z = a and z = b. This is the required probability.
If both limits a and b are positive or negative, we find the areas corresponding to z = a and z = b and then the required area is the Difference between them. If one limit say a is negative and other say b is positive then the areas from z = -a to z = 0 is the same as from z = 0 to z = a. We find it from the table and also from z = 0 to z = b from the table. Then the required area is the SUM of these two areas. If we want to find the expected frequency of variate x within certain limits when the experiment is carried for N times. Then first we find probability P which is equal to the area between the limits. Thus it is NP.
[next page]
|