1.6 Transversal across two parallel lines
Corresponding Angles : If a transversal
cuts two parallel lines the corresponding angles are equal ( figure
1.26 )
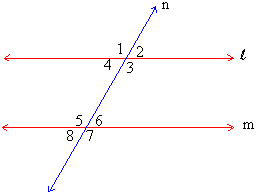
Figure 1.26
l & m are two parallel lines cut by a transversal n to form angles 1 to 8.
Axiom : Corresponding angles are equal in measure if a transversal cuts parallel lines.
m Ð 1 = m Ð 5
m Ð 2 = m Ð 6
m Ð 3 = m Ð 7
m Ð 4 = m Ð 8 .
Alternate interior angles : If a transversal
cuts two parallel lines the alternate interior angles are equal
in measure. In figure 1.26 m Ð 4
= m Ð 6 and m Ð
3 = m Ð 5. This can be proved as
follows :
m Ð 3 = m Ð 4 are supplementary and so also
m Ð 6 = m Ð 7 are supplementary.
Since the sums of their measures are 1800 in both cases.
m Ð 3 + m Ð 4 = m Ð 6 + m Ð 7.
However m Ð 3 = m Ð 7 as they are corresponding angles formed by a transversal across parallel lines.
Therefore, m Ð 3 + m Ð 4 = m Ð 6 + m Ð 3 i.e. m Ð 4 = m Ð 6.
Similarly it can be shown that m Ð 3 = m Ð 5 .
Alternate exterior angles : If a transversal
cuts two parallel lines the alternate exterior angles are equal
in measure. In figure 1.26 m Ð 1=
m Ð 7 and m Ð
2 = m Ð 8. This can be easily shown
as follows :
m Ð 1 = m Ð 3 (vertical angles)
m Ð 3 = m Ð
7 (corresponding angles on parallel lines)
\ mÐ
1 = m Ð 7
Consecutive Interior and Consecutive Exterior
Angles : If a transversal cuts two parallel lines the consecutive
interior angles and consecutive exterior angles are supplementary.
In figure 1.26 m Ð 4 and m Ð
5 are supplementary and also m Ð
3 and m Ð 6 are supplementary. This
is proven as :
m Ð 1 and m Ð 4 are supplementary
but m Ð 1 = m Ð 5 (corresponding angles on parallel lines )
\ m Ð 4 and m Ð 5 are supplementary.
Since consecutive exterior angles are supplementary. m Ð 1 and m Ð 8 so also
m Ð 2 and m Ð 7 should be supplementary.
Proof : m Ð 1 and m Ð
4 are supplementary but
m Ð 4 = m Ð 8 (corresponding angles on parallel lines )
\ m Ð 1 and m Ð 8 are supplementary.
|