1.7 Conditions for parallelism
Parallel lines are defined as those lines which are coplanar and do not intersect (figure 1.27). The figure merely show a part of the lines as the lines actually extend upto infinity. Hence although they do not intersect in the region that is observed it is possible that they will intersect when sufficiently extended.
In practice however the lines cannot be extended beyond the paper. Therefore it is not convenient to test parallelism by looking for a point of intersection.
Figure 1.27
If however a transversal is drawn across lines
l and m figure 1.28 all
the eight angles formed can be measured.
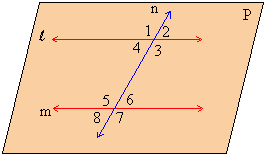
Figure 1.28
By using properties of these angles that are given
in section 1.6 line l
and m can be shown to be parallel.
Lines l
and m are parallel if :
1) corresponding angles formed by line n are equal in measure,
2) alternate interior angles are equal in measures,
3) the measures of alternate exterior angles are equal,
4) consecutive interior angles are supplementary,
5) consecutive exterior angles are supplementary.
These are called conditions for parallelism.
|