1.4 Some special angles

Complementary angles : If the sum of two angles equals 90⁰ the two angles are called complementary. Complementary angles thus add up to a right angle.

Complementary angles are of two types. If they have one side in common they are called adjacent complementary angles ( figure 1.20 a ). If no side is common then they are called non-adjacent complementary angles ( figure 1.20 b ).

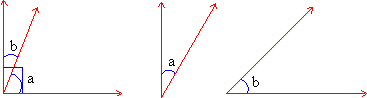
    Figure 1.20 a                          Figure 1.20 b

Since the measures of complementary angles always sum up to 90⁰ if the measure of one angle is known that of the complement can be found easily. In figure 1.20 b Ð a and Ð b are complementary. Also it is known that m Ð a = 30⁰.

m Ð a + m Ð b = 90⁰

    30⁰ + m Ð b = 90⁰

              m Ð b = 90⁰ - 30⁰

              m Ð b = 60⁰

Theorem : If two angles are complementary to a third angle, then they are equal to each other.

Proof : Ð a and Ð b are both complementary to Ð c.

\ m Ð a + m Ð c = 90⁰ and also

m Ð b + m Ð c = 90⁰

\ m Ð a + m Ð c = m Ð b + m Ð c OR

m Ð a = m Ð b

Index

Introduction

1.1 Points, Lines and Planes
1.2 Line Segment
1.3 Rays and Angles
1.4 Some Special Angles
1.5 Angles made by a Transversal
1.6 Transversal Across Two Parallel Lines
1.7 Conditions for Parallelism

Chapter 2