7.2 Lines of a Circle
The lines in the plane of the circle are classified into three categories (figure 7.2).
a) Lines like
l which do not
intersect the circle.
b) Lines like m which intersect the circle at only one point.
c) Lines like n which intersect the circle at two points..
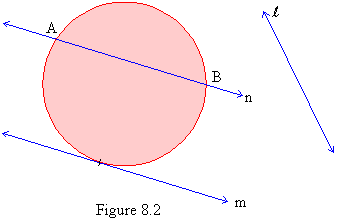Figure 8.2 Lines like m are called tangents. A tangent is a line that has one of its points on a circle and the rest outside the circle.
Line n is called a secant of the circle. A secant is defined as any line that intersects a circle in two distinct points.
A segment whose end points lie on a circle is called a Chord . In figure 7.2 AB is a chord of the circle. Thus a chord is always a part of secant. A circle can have an infinite number of chords of different lengths (figure 7.3)
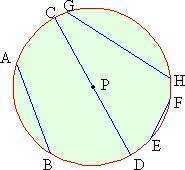
Figure 7.3 The longest chord of the circle passes through its center and is called as the diameter. In figure 7.3 chord CD is the diameter. It can be noticed immediately that the diameter is twice the radius of the circle. The center of the circle is the mid point of the diameter. A circle has infinite diameters and all have the same length.
Example 1
A, B, C & D lie on a circle with center P. Classify the following segments as radii and chords.
PA, AB, AC, BP, DP, DA, PC, BC, BD, CD.
Solution:
Example 2
Name the secant and the tangent in the following figure :
Solution:
secant - l
tangent - m
Example 3
P is the center of a circle with radius 5 cm. Find the length of the longest chord of the circle.
Solution:
10 cm.
If r = 5 cm d = 2r = 10 cm.
Diameter is the longest chord.
Therefore length of longest chord = 10 cm.
|
