7.8 Lengths of arcs and areas of sectors
An arc is a part of the circumference of the circle; a part proportional to the central angle.
If 3600
corresponds to the full circumference. i.e. 2 p
r then for a central angle of x0
(figure 7.24) the corresponding arc length will be
l such that
Figure 7.24
Analogically consider the area of a sector.
This too is proportional to the central angle. 3600
corresponds to area of the circle
p r2.
Therefore for a central angle m0
the area of the sector will be in the ratio :
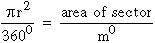
Example 1
In a circle with the radius of 2 cm, the central
angle for an arc AB is 750.
Find l
(seg.AB). Also find the area of the sector AOB having a central
angle of 750
Solution:
l
(seg AB) = 2.6
**********
|