7.3 Arcs
The angle described by any two radii of a circle
is called the central angle. Its vertex is the center of the circle.
In figure 8.4 Ð APB is a central
angle. The part of the circle that is cut by the arms of the central
angle is called an arc. AB is an arc and so is AOB . They are represented
as 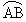 & &
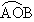 . .
Figure 7.4
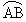 is called the minor arc and is called the minor arc and 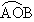 is the major arc. The minor arc is always represented by using the two end points of the arc on the circle. However it is customary to denote the major arc using three points. The two end points of the major arc and a third point also on the arc. If a circle is cut into two arcs such that there is no minor or major arc but both the arcs are equal then each arc is called a semicircle. is the major arc. The minor arc is always represented by using the two end points of the arc on the circle. However it is customary to denote the major arc using three points. The two end points of the major arc and a third point also on the arc. If a circle is cut into two arcs such that there is no minor or major arc but both the arcs are equal then each arc is called a semicircle.
An arc is measured as an angle in degrees and also in units of length. The measure of the angle of an arc is its central angle and the length of the arc is the length of the portion of the circumference that it describes.
angle of an arc AB = m 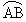
length of an arc AB = l 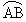
Since the measure of the angle of an arc is its central angle, if two central angles have equal measure then the corresponding minor arcs are equal.
Conversely if two minor arcs have equal measure then their corresponding central angles are equal.
|