7.7 Segments of chords secants and tangents
Theorem : If two chords, seg.AB and seg.CD
intersect inside or outside a circle at P then l
(seg. PA) ´
l
(seg. PB) = l (seg.
PC) ´
l (seg. PD)
Figure 7.21 (a) Figure 7.21 (b)
In figure 7.21 (a) P is in the interior of
the circle. Join AC and BD and consider DAPC
and DBDP.
m Ð
APC = m Ð BPD (vertical
angles).
m Ð
CAP = m Ð BDP (angles
inscribed in the same arc).
\
DAPC
~ D
BPD ( A A test )
 \
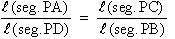( corresponding sides of similar triangles).
l (seg.
PA) ´
l
(seg. PB) = l (seg.
PC) ´
l (seg. PD).
Now consider figure 7.21 (b).
P is in the exterior of the circle. Join A to C and B to D.
Consider D
PAC and D PBD
m Ð
APC = m Ð BPD (same
angle).
m Ð
CAP = m Ð PDB
(exterior angle property of a cyclic quadrilateral).
\
D
PAC ~ D
PDB ( A A test )
\
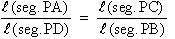(corresponding sides of similar triangles).
\
l (seg.
PA) ´
l
(seg. PB) = l (seg.
PC) ´
l (seg. PD).
Consider a secant PAB to a circle, (figure 7.22) intersecting
the circle at A and B and line PT is a tangent then l
(seg. PA) ´
l
(seg. PB) = l (seg.
PT)2.
Figure 7.22
P is a point in the exterior of the circle. A secant passes through P and intersects the circle at points A & B. Tangent through P touches the circle in point T.
To prove that l
(seg. PA) ´
l
(seg. PB) = l (seg.
PT)2
Consider D
PTA and D PTB.
m Ð
TPA = Ð TPB (
same angle)
According to Tangent Secant theorem,
m Ð ATP
= 
m (arc AT)
= m
Ð PTB ( inscribed
angle )
\
D
PTA ~ D PTB ( A A
test )
 \
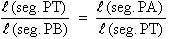(corresponding sides of similar triangles).
\
l (seg.
PA) ´
l
(seg. PB) = l (seg.
PT)2.
Theorem: The lengths of two tangent segments from an external point to a circle are equal.
As shown in figure 7.23 seg. QR and seg. QS are two tangents on a circle with P as its center.
Figure 7.23
To prove that
l (seg.QR) =
l (seg.QS) join P to Q and R to S.
m Ð
PRQ = m Ð
PSQ = 900.
The radius and the tangent form a right angle at the point of tangency,
\
D
PRQ and D PSQ are right
triangles such that
seg. PR @
seg PS (radii of the same circle).
seg. PQ @
seg. PQ (same side).
\
D
PRQ @
D PSQ (H.S)
\
seg.QR @ seg.QS (corresponding
sides of congruent triangles are congruent).
\
l
(seg.QR) = l
(seg.QS).
|
