15.5 Carnot Cycle

Since heat is a form of energy, its conversion to other forms of energy should be possible. The discovery that heat can be converted into mechanical energy was one of the most important cases that let to the Industrial Revolution in the 19th century.

The first law of Thermodynamics allows for the conversion of heat energy into mechanical energy in the same amount. However in order to be able to convert heat energy into mechanical energy in a continuous manner it is necessary to restore the working substance in a device called the heat engine. These device converts heat energy into mechanical energy- back to its original state by taking it through a reversible cyclic process. This cyclic process can operate by transferring some amount of the heat energy absorbed. Thus only a part of the heat energy absorbed is found to be convertible into mechanical energy.

If some enclosed gas is made to absorb heat isothermally, for example, then it will expand and the work done by the gas can be used as mechanical energy but unless the gas is brought back to its starting condition it cannot continue to convert heat energy into mechanical energy. Now, if it is brought back to its original state by compressing it along the reverse path then obviously the mechanical energy obtained during expansion will have to be spent in converting into heat energy; thus the net amount of mechanical energy obtained will be nil.

Therefore, in any heat engine the working substance operates between a source of heat at a higher temperature and a sink of heat at lower energy. Only the difference of heat energy absorbed from a source (or reservoir) and the heat energy transferred to the sink can be converted into mechanical energy. This is true even if the heat engine, i.e. an ideal engine that is no dissipation of energy is assumed to occur. Such an ideal engine is called Carnot's engine and it operates in a Carnot reversible cycle. The working substance used in this is an ideal gas.

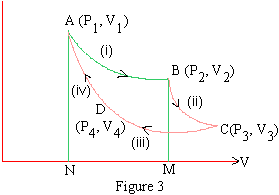
The Carnot cycle operates in this manner. The ideal gas of a fixed mass is enclosed in a cylindrical vessel by means of a lightly fitting piston. The mass of the vessel and piston are frictionless. The walls are nonconducting; the base is conducting over which a nonconducting cap can be mounted whenever required. Also a reservoir or a source of heat at temperature T₁⁰K of an unlimited capacity and a sink of heat at temperature T₂⁰K (T₁ > T₂) (also of unlimited capacity) are available.

1. Assume the gas to be in the initial state P₁, V₁ at temperature T₁ . Let it be placed in thermal contact with the reservoir and allowed to expand isothermally to state P₂ , V₂ - absorbing heat energy of amount Q₁ from the reservoir.

2. Take the gas away from reservoir, mount a nonconducting cap on its base, and let it continue to expand adiabatically to the state P₂, V₂ at T⁰ K.

3. Now, remove the nonconducting cap and put the gas in thermal contact with sink at T₂⁰ K and compress it isothermally to the state P₃, V₃.

4. Finally, disengage the gas from the sink and mount the non- conducting cap on the base of the cylinder and compress the gas adiabatically to the state P₁, V₁ and T₁⁰ K.

Thus the cycle is complete and gas comes back to the initial state P₁, V₁ at T₁⁰ K. Periodically the cycle of operations (i) and (iv) is repeated to continuously keep on obtain mechanical energy from heat energy.

The cycle is represented on the P- V (indicator) diagram in figure. 3.

Index

15.1 The Zeroth Law
15.2 The First Law
15.3 Work done and Some applications of First Law
15.4 Thermodynamic Processes
15.5 Carnot Cycle
15.6 The Second Law
15.7 Entropy

  Chapter 16