|
5.6 Co-efficient Of Variation ( C. V. )
To compare the variations ( dispersion ) of two different series, relative measures of standard deviation must be calculated. This is known as co-efficient of variation or the co-efficient of s. d. Its formula is
C. V. = 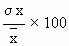
Thus it is defined as the ratio s. d. to its mean.
Remark: It is given as a percentage and is used to compare the consistency or variability of two more series. The higher the C. V. , the higher the variability and lower the C. V., the higher is the consistency of the data.
Example Calculate the standard deviation and its co-efficient from the following data.
|
A |
10 |
|
B |
12 |
|
C |
16 |
|
D |
8 |
|
E |
25 |
|
F |
30 |
|
G |
14 |
|
H |
11 |
|
I |
13 |
|
J |
11 |
Solution :
|
No
No. |
xi |
(xi - x) |
( xi - x )2 |
|
A |
10 |
-5 |
25 |
|
B |
12 |
-3 |
9 |
|
C |
16 |
+1 |
1 |
|
D |
8 |
-7 |
49 |
|
E |
25 |
+10 |
100 |
|
F |
30 |
+15 |
225 |
|
G |
14 |
-1 |
1 |
|
H |
11 |
-5 |
16 |
|
I |
13 |
-2 |
4 |
|
J |
11 |
-4 |
16 |
|
n= 10 |
S xi = 150 |
|
S |xi - x |2 = 446 |
Calculations :
i) 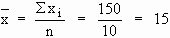
ii) 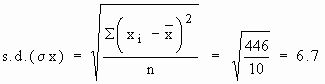
iii) 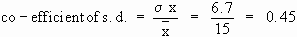
[next page]
|
Index
5.1 Introduction
5.2 Methods of computing dispersion
5.3 Range
5.4 Mean Deviation
5.5 Variance
5.6 Coefficient of Variation
5.7 Percentile
5.8 Quartiles and interquartile range
5.9 Skewness moments and Kurtosis
5.10 Kurtosis
Chapter 6
|