If we concentrate on two extreme values ( as in the case of range ), we don’t get any idea about the scatter of the data within the range ( i.e. the two extreme values ). If we discard these two values the limited range thus available might be more informative. For this reason the concept of interquartile range is developed. It is the range which includes middle 50% of the distribution. Here 1/4 ( one quarter of the lower end and 1/4 ( one quarter ) of the upper end of the observations are excluded.

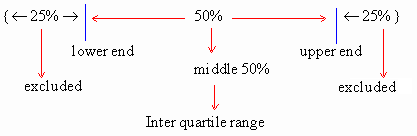
Now the lower quartile ( Q₁ ) is the 25th percentile and the upper quartile ( Q₃ ) is the 75th percentile. It is interesting to note that the 50th percentile is the middle quartile ( Q₂ ) which is in fact what you have studied under the title ’ Median ". Thus symbolically

Inter quartile range = Q₃ - Q1

If we divide ( Q₃ - Q₁ ) by 2 we get what is known as Semi-Iinter quartile range.

i.e. 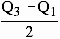. It is known as Quartile deviation ( Q. D or SI QR ).

Therefore Q. D. ( SI QR ) =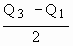

[next page]

Index

5.1 Introduction
5.2 Methods of computing dispersion
5.3 Range
5.4 Mean Deviation
5.5 Variance
5.6 Coefficient of Variation
5.7 Percentile
5.8 Quartiles and interquartile range
5.9 Skewness moments and Kurtosis
5.10 Kurtosis

Chapter 6