|
5.9 Skewness, Moments And Kurtosis
The voluminous raw data cannot be easily understood, Hence, we calculate the measures of central tendencies and obtain a representative figure. From the measures of variability, we can know that whether most of the items of the data are close to our away from these central tendencies. But these statical means and measures of variation are not enough to draw sufficient inferences about the data. Another aspect of the data is to know its symmetry. in the chapter "Graphic display" we have seen that a frequency may be symmetrical about mode or may not be. This symmetry is well studied by the knowledge of the "skewness." Still one more aspect of the curve that we need to know is its flatness or otherwise its top. This is understood by what is known as " Kurtosis."
Skewness
It may happen that two distributions have the same mean and standard deviations. For example, see the following diagram.
Click here to enlarge
Although the two distributions have the same means and standard deviations they are not identical. Where do they differ ?
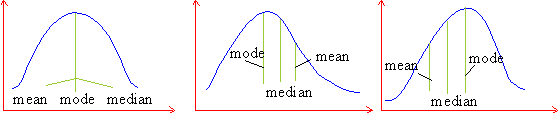
They differ in symmetry. The left-hand side distribution is
symmetrical one where as the distribution on the right-hand is asymmetrical
or skewed. For a symmetrical distribution, the values, of equal
distances on either side of the mode, have equal frequencies. Thus,
the mode, median and mean - all coincide. Its curve rises slowly,
reaches a maximum ( peak ) and falls equally slowly (Fig. 1). But
for a skewed distribution, the mean, mode and median do not coincide.
Skewness is positive or negative as per the positions of the mean
and median on the right or the left of the mode.
A positively skewed distribution ( Fig.2 ) curve rises rapidly, reaches the maximum and falls slowly. In other words, the tail as well as median on the right-hand side. A negatively skewed distribution curve (Fig.3) rises slowly reaches its maximum and falls rapidly. In other words, the tail as well as the median are on the left-hand side.
Click here to enlarge
|
Size |
Frequency |
Size |
Frequency |
Size |
Frequency |
|
1 |
12 |
1 |
4 |
1 |
3 |
|
2 |
13 |
2 |
6 |
2 |
7 |
|
3 |
14 |
3 |
12 |
3 |
8 |
|
4 |
15 |
4 |
10 |
4 |
10 |
|
5 |
14 |
5 |
8 |
5 |
12 |
|
6 |
13 |
6 |
7 |
6 |
6 |
|
7 |
12 |
7 |
3 |
7 |
4 |
[next page]
|
Index
5.1 Introduction
5.2 Methods of computing dispersion
5.3 Range
5.4 Mean Deviation
5.5 Variance
5.6 Coefficient of Variation
5.7 Percentile
5.8 Quartiles and interquartile range
5.9 Skewness moments and Kurtosis
5.10 Kurtosis
Chapter 6
|