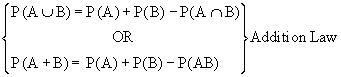
Clearly, the outcomes of both A and B are non-mutually exclusive.
Example Two dice are rolled. Find the
probability that the score is an even number or multiple of 3.
Solution : Two dice are rolled.
Sample space = {(1, 1), (1, 2), ............,
(6, 6)}
n(S) = 6
´ 6 = 36
Event E : The score is an even number or multiple of 3.
Note here score means the sum of the numbers on both the dice when they land. For example (1, 1) has score 1 + 1 = 2.
It is clear
that the least score is 2 and the highest score (6, 6) Þ
6 + 6 = 12
i.e. score 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
Let Event A : Score is an even numbers
A = {(1, 1), (1, 3), (1, 5), (2,2),
(2, 4), (2, 6), (3, 1), (3, 3) (3,
5), (4, 2), (4, 4), (4, 6), (5, 1), (5, 3), (5, 5), (6, 2), (6,
4), (6, 6) }
Therefore n (A) = 18
Let Event B: The score is the multiple of 3
i.e. 3, 6, 9, 12
B = {(1, 2), (1, 5), (2, 4), (2,
1) (3, 6) (3, 3) (4,2), (4, 5), (5,
1), (5,4), (6, 3), (6, 6) }
n (B) = 12
Let Event A ÇB:The
score is an even number and multiple of 3 or (i.e.
common to both A and B) AB
AB = {(2, 4), (4, 2), (33,3), (4,2), (5, 1), (6,6)}
n (AB) = 6
[next page]
|
Index
7. 1 Introduction
7.2 Trial
7.3 Sample Space
7. 4 Definition of Probability
7. 5 The Laws of Probability
7. 6 Conditional Probability
7. 7 Theoretical Distribution
7. 8 Binomial Distribution
7. 9 Normal Distribution
Chapter 8
|