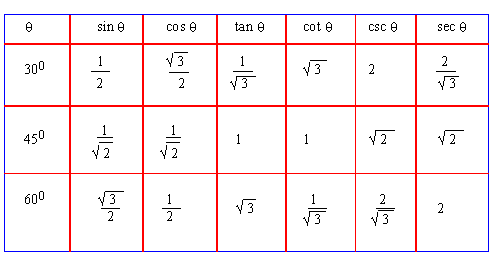
|
Click here to enlarge
SOLVED PROBLEMS
- In D ABC, Ð
B = 900, BC = 1, AC = 2. Find Ð
A, ÐC and AB.
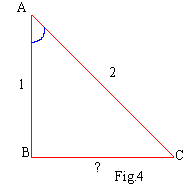
Solution
cos C = 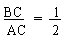
cos C = cos 600 ..... [From
the table]
\Ð C = 600
\Ð A = 600
and by the Pythagoras theorem, AB2 = AC2 - BC2
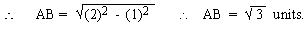
-
Triangle ABC is isosceles with Ð
B = Ð C = p
/ 6 rad. AD is the median meeting BC in point D. Find AD and
AB. Given that BC = 6 cms.
Solution
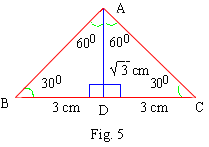
SinceÐ B =Ð
C= p / 6 rad = 300
Since D ABC is an isosceles triangle,
median AD is perpendicular to side BC
Also BD = DC = 3 cm and Ð BAD =
Ð CAD = 600
|
Index
2.1 Trigonometric Ratio of Acute Angles
2.2 Fundamental Relation between the trigonometric Ratios of an angle
2.3 Functions of General Angles or t Ratio
2.4 Tables of Trigonometric Function
Supplementary Problems
Chapter 3
|