|
Now tan 300 = 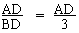
\ AD = 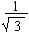 ´3 = Ö
3
´3 = Ö
3
Also by the theorem of pythagoras, AB2= AD2
+ BD2
\ AB2
= (3)2 + ( Ö 3 ) 2
= 12 \ AB = 2 Ö
3
-
Find the values of t- ratios of the acute
angles of the right triangle ABC, given a = 2, c = 2 Ö
5 .
Solution
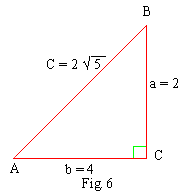
Since b2 = c2 - a2 = (2 Ö
5 )2 - (2)2 = 20 - 4 = 16 \
b = 4
then sin A = 2 / 2 Ö 5 = 1 / Ö
5 = Ö 5 / 5 = cos B
cos A = 4 / 2 Ö 5 = 2 / Ö
5 = 2 Ö 5 / 5 = sin B
tan A = 2 /4 = 1/2 = cot B
cot A = 4 /2 = 2 = tan B
sec A = 2 Ö 5 / 4 = Ö5
/ 2 = csc B
csc A = 2 Ö 5 / 2 = Ö
5 = sec B
-
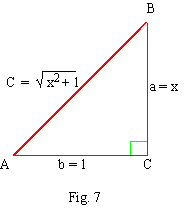
If A is acute angle and tan A = x. Determine
the values of the remaining t - ratios.
Solution
 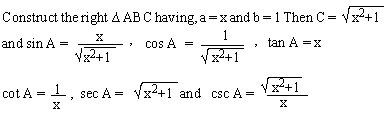
- A 6 foot electric cord is stretched taut from the bottom of
a clock on a wall to a socket on the same wall. The socket is
1-foot above the floor. If you draw a line from the clock straight
down to the floor. The floor would make an angle with the cord
whose cosine is 0.9. How high above the floor is the bottom of
the clock ?
|