|
3.4 The Ambiguous Case Of The Law Of Sines
If two sides and one angle opposite to one of
them are given, there can be complications in solving triangles.
In fact, from the given data, we may determine more than one triangle
or perhaps no triangles at all.
Let the angle be C and sides be c and b of triangle
ABC given then
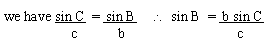
Here, R.H.S. is completely known and hence Ð
B can be found out.
Also Ð C is given \
ÐA = 1800 - (B + C).
Thus triangle ABC is solved.
But when sin B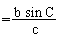 
has R. H.S. with such values that the triangle can't be com pleted.
Observe,
(I) When Ð C < 900 (acute angle)
(a) If c < b sin C then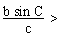 
1 i.e. sin B > 1 which is impossible (as sine c ratio never exceeds
1)
(b) c = b sin C then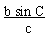 
= 1 i.e. sin B = 1 \ Ð
B = 900 i.e triangle ABC is c right triangle.
(c) If c > b sin C then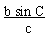
< 1 i.e. sin B < 1. But within the range 00 to
1800 ; there are two values of angles for a sine ratio
as sin q = sin (180 - q),
of which one is acute and the other is an obtuse. e.g. sin 300
= sin 1500
But both of these may not be always admissible.
If ÐB < 900
(acute), the triangle ABC is possible as c > b then Ð
C > Ð B. But if Ð
B > 900 (obtuse) then Ð
C will be also obtuse ; this is impossible as there can't be two
obtuse angles in a triangle.
If c < b and Ð
C is acute then both values of B are admissible . Naturally there
will be two values of Ð A and hence
two values of a. Hence there are two triangle possible.
(II) When Ð C
< 900 (obtuse angle).
Here (1) If c < b then Ð
C < Ð B but then B will also
become an obtuse angle. It is also impossible.
(2) If c = b then Ð
B = Ð C. Hence Ð
C is obtuse makes Ð B obtuse too
which again impossible.
(3) If c > b then Ð
C > Ð B. But again there are
two possibilities (i) Ð B is acute
(ii) and Ð B is obtuse.
If Ð B is acute
the triangle is possible and when Ð
B is obtuse the triangle is impossible. For the obtained values
of the elements when there is ambiguity (i.e. we are unable to draw
such a triangle) to determine the triangle ; it is called an 'ambiguous
case'.
[next page]
|
