|
Now we are in position to define circular functions (sine, cosine, tangent,
cotangent, secant and cosecant) of the real number t. Let P(x, y) is point on the unit circle such that
AP = t then
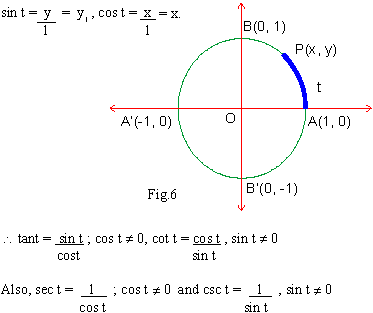
Note : P(x,y) is now P(cos t, sin t). This clearly indicates that the range
is restricted. For the sine and cosine, the abscissa (x-coordinate) of a point which revolves round the unit circle,
vary between -1 and 1 and the ordinate (y-coordinate) too varies between -1 and 1. Therefore
the range of Sine and Cosine functions is a set of real numbers 'Z' such that -1
£ Z £ 1.
EXAMPLE 1
What are the values of 't' in the domain of sine and cosine functions between
-2p and 2p, having range values of 1?
Solution
The range of sin t = 1 (given)
Let the point P (cos t, sin
t). For P, sin t = 1. then P must be P (0,1) on the unit circle. This occurs
when 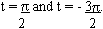
The range of cos t = 1 (given)
Let the point P (cos t, sin t).
For P, cos t = 1. The point P must be P (1,0) on the unit circle. This occurs when
t = 0 and t = 2p.
EXAMPLE 2
The trigonometric point P(t) has coordinates 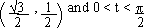 Find 't' Find 't'
Solution : P(t) is 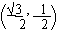 , then the values of sin t and cos t follows from the definitions as
follows: , then the values of sin t and cos t follows from the definitions as
follows:
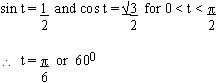
EXAMPLE 3
The point P(2/3, -1/3) is on the unit circle. From A(1,0) arc AP is 't' find the values
(ranges) of six circular functions of t.
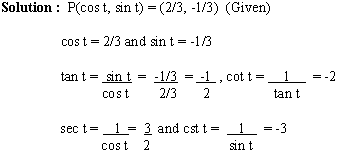
|
Index
5.
1 Circular function
5.
2 Periodic function
5.
3 Even & Odd
5.4
Graphs of Trigonometric Functions
Supplementary
Problems
Chapter 6
|