|
5.3 Even & Odd
(1) Even Function
A function f (t) is said to be
'Even' when it satisfies the condition f (-t) = f
(t)
For example, cos (-t) = cos t, sec (-t) = sec t are even circular functions.
It should be noted that the graph of an even function is symmetrical about the vertical.
(i.e. y axis.)
(2) Odd Function
A function f (t) is said to be
'Odd' when it satisfies the condition f (-t) = -f (t)
For example, sin (-t) = -sin t, csc (-t) = -csc
tan (-t) = -tan t, cot (-t) = -cot (t)
are 'odd' circular functions.
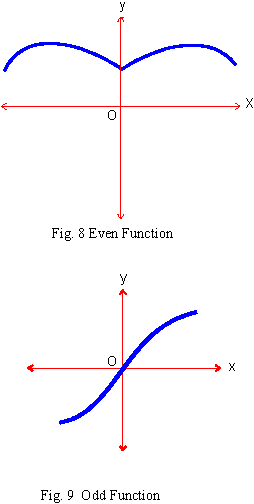
It should be noted that the graph of an odd function is symmetrical about the origin of
the rectangular coordinate system.
(i) product of two even functions is an even function.
(ii) product of two odd functions is an even function.
(iii) product of an even and an odd function is an odd function.
(iv) Any function f(t) can be expressed as the sum of two component functions of which one
is even [f e(t)] and the other is odd
[fo (t)]
Thus f(t) = f e(t) + fo (t)
(v) The sum of an odd and an even function is neither even nor odd.
|